题目内容
【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)
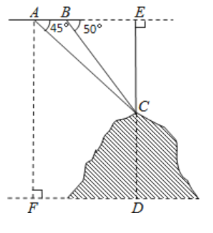
(1)直接写出∠ACB的大小;
(2)求这座山的高度CD.
【答案】(1)∠ACB=5°;(2)这座山的高度约是1900米.
【解析】
(1)利用三角形内角和定理求得∠ACE、∠BCE的大小,结合图形求得答案;
(2)设EC=x,则在RT△BCE中,可表示出BE,在Rt△ACE中,可表示出AE,继而根据AB+BE=AE,可得出方程,解出即可得出答案.
解:(1)如图,在直角△AEC中,∠ACE=90°﹣45°=45°.
在直角△BEC中,∠BCE=90°﹣50°=40°.
则∠ACB=∠ACE﹣∠BCE=45°﹣40°=5°;
(2)设EC=x,
在Rt△BCE中,tan∠EBC=![]() ,
,
则BE=![]() =
=![]() x,
x,
在Rt△ACE中,tan∠EAC=![]() ,
,
则AE=![]() =x,
=x,
∵AB+BE=AE,
∴300+![]() x=x,
x=x,
解得:x=1800,
这座山的高度CD=DE﹣EC=3700﹣1800=1900(米).
答:这座山的高度约是1900米.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】某自行车经营店销售![]() 型,
型,![]() 型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
|
| |
进货价格(元/辆) | 1000 | 1100 |
销售价格(元/辆) |
| 1500 |
今年经过改造升级后,![]() 型车每辆销售价比去年增加400元.已知
型车每辆销售价比去年增加400元.已知![]() 型车去年1月份销售总额为3.6万元,今年1月份
型车去年1月份销售总额为3.6万元,今年1月份![]() 型车的销售数量与去年1月份相同,而销售总额比去年1月份增加
型车的销售数量与去年1月份相同,而销售总额比去年1月份增加![]() .
.
(1)若设今年1月份的![]() 型自行车售价为
型自行车售价为![]() 元/辆,求
元/辆,求![]() 的值?(用列方程的方法解答)
的值?(用列方程的方法解答)
(2)该店计划8月份再进一批![]() 型和
型和![]() 型自行车共50辆,且
型自行车共50辆,且![]() 型车数量不超过
型车数量不超过![]() 型车数量的2倍,应如何进货才能使这批自行车获利最多?
型车数量的2倍,应如何进货才能使这批自行车获利最多?
(3)该店为吸引客源,准备增购一种进价为500元的![]() 型车,预算用8万元购进这三种车若干辆,其中
型车,预算用8万元购进这三种车若干辆,其中![]() 型与
型与![]() 型的数量之比为
型的数量之比为![]() ,则该店至少可以购进三种车共多少辆?
,则该店至少可以购进三种车共多少辆?
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )的自变量x与函数值y的部分对应值如下表:
)的自变量x与函数值y的部分对应值如下表:
| … | -1 | 0 | 1 | 3 | … |
| … |
| 3 |
| 3 | … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②3是关于
;②3是关于![]() 的方程
的方程![]() 的一个根;③
的一个根;③![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A.0B.1C.2/span>D.3