我们都有这样的生活经验.要想使多边形木架不变形至少再钉上若干根木条.如图所示.四边形至少再钉上一根,五边形至少再钉上两根,六边形至少再钉上三根,-.按照此规律.十边形至少再钉上( )A．9根B．8根C．7根D．6根题目和参考答案——青夏教育精英家教网—

题目内容

9．我们都有这样的生活经验，要想使多边形（三角形除外）木架不变形至少再钉上若干根木条，如图所示，四边形至少再钉上一根；五边形至少再钉上两根；六边形至少再钉上三根；…，按照此规律，十边形至少再钉上（　　）

A．

9根

B．

8根

C．

7根

D．

6根

分析根据分成三角形个数与边数的关系，需要的木条数等于过多边形的一个顶点的对角线的条数，由此得出答案即可．

解答解：过n边形的一个顶点可以作（n-3）条对角线，把多边形分成（n-2）个三角形，
所以，要使一个十边形木架不变形，至少需要10-3=7根木条固定．
故选：C．

点评此题考查图形的变化规律，考虑把多边形分成三角形是解题的关键．

练习册系列答案

20．等腰三角形一腰上的高与底边的夹角为40°，则顶角的度数为（　　）

17．

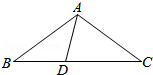如图，在△ABC中，D是BC上一点，若∠B=∠C=∠BAD，∠DAC=∠ADC，∠BAC的度数为（　　）

4．（1）$（3{x^2}y-x{y^2}+2xy）÷\frac{1}{2}xy$
（2）（ab²）²•（-a³b）³÷（-5ab）．

14．[问题情境]
将一副直角三角板（Rt△ABC和Rt△DEF）按如图1所示的方式摆放，其中∠ACB=90°，CA=CB，∠FDE=90°，O是AB的中点，点D与点O重合，DF⊥AC于点M，DE⊥BC于点N，连接MN，试判断△OMN与△CBA是否相似，并说明理由．

[探究展示]
小明同学展示如下正确的解法：
解：△OMN∽△CBA，证明如下：
∵CA=CB，∴∠A=∠B．
∵O是AB的中点，∴OA=OB．
∵DF⊥AC于点M，DE⊥BC于点N，∴∠AMO=∠BNO=90°．
∵在△OMA与△ONB中，$\left\{\begin{array}{l}{∠AMO=∠BNO}\\{∠A=∠B}\\{OA=OB}\end{array}\right.$
∴△OMA≌△ONB（依据1）．
∴OM=ON．
∵CA=CB，∴$\frac{OM}{CA}$=$\frac{ON}{CB}$．
又∵∠MON=∠ACB，
∴△OMN∽△CBA（依据2）．
[反思交流]
（1）上述证明过程中的“依据1”和“依据2”分别指的是什么？
依据1：AAS；
依据2：两组对应边成比例且夹角相等的两个三角形相似．
（2）将图1中的Rt△DEF沿着射线BA的方向平移，使点D落在BA的延长线上，FD的延长线与CA的延长线垂直相交于点M，BC的延长线与DE垂直相交于点N，连接OM，ON，MN，如图2所示，试判断△OMN的形状，并注明你的结论；
（3）将图1中的Rt△DEF沿着射线AB的方向平移，使点D落在AB的延长线上，直线FD与直线CA垂直相交于点M，直线BC与直线DE垂直相交于点N，连接OM，ON，MN，如图3所示，试判断△OMN的形状，并注明你的结论．

1．在平面直角坐标系中，若点M（2，3）与点N（2，y）之间的距离是4，则y的值是（　　）

18．等腰三角形的一边长是3cm，其中一边长为4cm，其它周长分别为（　　）

19．

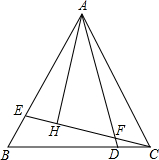如图，△ABC是等边三角形，点D、E分别是BC边、AB边上的点，且BE=CD，连接AD、CE交于点F，过A作AH⊥CE于H，
（1）求证：∠BCE=∠CAD；
（2）直接写出∠CFD的度数；并写出线段AF与线段HF的数量关系．（无需解答过程）

试题分类