题目内容
19. 如图,⊙O的直径CD过弦EF的中点G,且CD=10,EF=8,则tan∠C=$\frac{1}{2}$.
如图,⊙O的直径CD过弦EF的中点G,且CD=10,EF=8,则tan∠C=$\frac{1}{2}$.
分析 ⊙O的直径CD过弦EF的中点G,故EG=FG=$\frac{1}{2}$×8=4,根据垂径定理得CD⊥EF,再根据勾股定理得出OG的长,得CG的长,根据锐角三角函数的定义即可得出结论.
解答 解:∵⊙O的直径CD过弦EF的中点G,
∴EG=FG=$\frac{1}{2}$×8=4,CD⊥EF,
∵CD=10,
∴OC=OE=5,
∴OG=$\sqrt{{OE}^{2}{-EG}^{2}}$=$\sqrt{{5}^{2}{-4}^{2}}$=3,
∴CG=8,
∴tan∠C=$\frac{FG}{CG}$=$\frac{4}{8}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查了垂径定理,锐角三角函数的定义及勾股定理,熟知平分弦的直径垂直于弦是解答此题的关键.

练习册系列答案
相关题目
9.把351000用科学记数法表示,正确的是( )
| A. | 0.35×104 | B. | 3.51×105 | C. | 3.51×104 | D. | 35.1×104 |
10.某货主租用汽车运输公司的甲、乙两种货车运货,两次租用的车辆数和运货数如下表所示,问甲、乙两种货车每次能运货多少吨?
| 第一次 | 第二次 | |
| 甲种货车车辆数(辆) | 5 | 2 |
| 乙种货车车辆数(辆) | 3 | 6 |
| 累计运货数(吨) | 37.5 | 39 |
8.在下列各数中,最小的数是( )
| A. | 1.00×10-9 | B. | 9.99×10-8 | C. | 1.002×10-8 | D. | 9.999×10-7 |
 如图所示,8个相同的长方形地砖拼成一个大长方形,则每块小长方形地砖的面积是300cm2.
如图所示,8个相同的长方形地砖拼成一个大长方形,则每块小长方形地砖的面积是300cm2.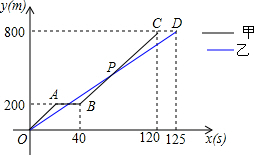 在800米跑步测试过程中,甲乙两名运动员同时起跑,刚跑出200米时甲不慎摔倒,他又迅速爬起来再次投入比赛,并最终超越乙取得优异成绩.图中分别表示甲、乙两名运动员所跑的路程y(m)与比赛时间x(s)之间的关系.
在800米跑步测试过程中,甲乙两名运动员同时起跑,刚跑出200米时甲不慎摔倒,他又迅速爬起来再次投入比赛,并最终超越乙取得优异成绩.图中分别表示甲、乙两名运动员所跑的路程y(m)与比赛时间x(s)之间的关系.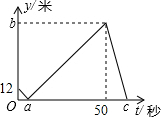 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步300米,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则以下结论:①a=6;②b=88;③c=72,其中正确的结论个数为( )
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步300米,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则以下结论:①a=6;②b=88;③c=72,其中正确的结论个数为( )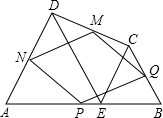 如图,在四边形ABCD中,E是AB上的一点,△ADE和△BCE都是等边三角形,点P、Q、M、N分别为AB、BC、CD、DA的中点,则四边形MNPQ是( )
如图,在四边形ABCD中,E是AB上的一点,△ADE和△BCE都是等边三角形,点P、Q、M、N分别为AB、BC、CD、DA的中点,则四边形MNPQ是( )