题目内容
5. 如图,在△ACB中,∠ACB=90°,CD⊥AB于D,E为CB上一点,连结AE,过E作EF⊥AE,交AB于点F.
如图,在△ACB中,∠ACB=90°,CD⊥AB于D,E为CB上一点,连结AE,过E作EF⊥AE,交AB于点F.(1)求证:△AOC∽△EFB.
(2)当E为BC中点且BC=2AC,求$\frac{EF}{OE}$的值.
分析 (1)由∠ACB=90°,CD⊥AB于D,得到∠ACD+∠CAB=∠CAB+∠B=90°,求出∠ACD=∠B,由于∠CAE+∠AEC=∠AEC+∠FEB=90°,得到∠CAE=∠FEB,于是得到结论;
(2)由E为BC中点且BC=2AC,得到AC=CE=BE,由于△AOC∽△EFB,推出△ACO≌△BEF,得到AO=EF,过O作OH⊥CE于H,证得△OHE是等腰直角三角形,得到OH=HE由于tan∠B=$\frac{AC}{BC}$=$\frac{1}{2}$,得到tan∠COH=$\frac{CH}{OH}$=$\frac{1}{2}$,通过$\frac{AO}{OE}=\frac{CH}{HE}=\frac{1}{2}$,于是得到结论
解答 (1)证明:∵∠ACB=90°,CD⊥AB于D,
∴∠ACD+∠CAB=∠CAB+∠B=90°,
∴∠ACD=∠B,
∵EF⊥AE,
∴∠CAE+∠AEC=∠AEC+∠FEB=90°,
∴∠CAE=∠FEB,
∴△AOC∽△EFB;
(2)解:∵E为BC中点且BC=2AC,
∴AC=CE=BE,
∵△AOC∽△EFB,
∴∠CAO=∠FEB,∠ACO=∠B,
在△ACO与△BEF中,$\left\{\begin{array}{l}{∠CAO=∠FEB}\\{AC=BE}\\{∠ACD=∠B}\end{array}\right.$,
∴△ACO≌△BEF,
∴AO=EF,
过O作OH⊥CE于H,
∵∠ACE=90°,
∴OH∥AC,
∴△OHE是等腰直角三角形,
∴OH=HE,∴∠COH=∠B,
∵tan∠B=$\frac{AC}{BC}$=$\frac{1}{2}$,
∴tan∠COH=$\frac{CH}{OH}$=$\frac{1}{2}$,
设CH=x,OH=EH=2x,
∴$\frac{AO}{OE}=\frac{CH}{HE}=\frac{1}{2}$,
∴$\frac{EF}{OE}$的值是$\frac{1}{2}$.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,等腰直角三角形的性质,熟练掌握现实世界是解题的关键.

| A. | (a-$\frac{1}{2}$b)(a-$\frac{1}{2}$b) | B. | (a-$\frac{1}{2}$b)(-a+$\frac{1}{2}$b) | C. | (a-$\frac{1}{2}$b)(-a-$\frac{1}{2}$b) | D. | (a+$\frac{1}{2}$b)(-a-$\frac{1}{2}$b) |
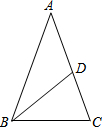 如图,在△ABC中,AB=AC=3,BC=2,点D在腰AC上,且BD=BC,那么CD=$\frac{4}{3}$.
如图,在△ABC中,AB=AC=3,BC=2,点D在腰AC上,且BD=BC,那么CD=$\frac{4}{3}$. 有理数a、b、c在数轴上的位置如图所示,化简|a+b|+|b+c|+|c+a|的结果是2a-2b-2c.
有理数a、b、c在数轴上的位置如图所示,化简|a+b|+|b+c|+|c+a|的结果是2a-2b-2c. 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D,若AC=7cm,BC=3cm,则△DBC的周长是10cm.
如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D,若AC=7cm,BC=3cm,则△DBC的周长是10cm. 如图,是一个6×6的棋盘,两人各持若干张1×2的卡片轮流在棋盘上盖卡片,每人每次用一张卡片盖住相邻的两个空格,谁找不出相邻的两个空格放卡片就算谁输,你用什么办法战胜对手呢?
如图,是一个6×6的棋盘,两人各持若干张1×2的卡片轮流在棋盘上盖卡片,每人每次用一张卡片盖住相邻的两个空格,谁找不出相邻的两个空格放卡片就算谁输,你用什么办法战胜对手呢?