题目内容
12. 如图,AB∥CD,CE平分∠ACD交AB于E,∠A=80°,则∠AEC=50°.
如图,AB∥CD,CE平分∠ACD交AB于E,∠A=80°,则∠AEC=50°.
分析 首先根据平行线的性质可得∠A+∠ACD=180°,∠AEC=∠ECD,再由条件∠A=80°可得∠ACD的度数,再根据角平分线的性质可得∠ECD的度数,进而可得答案.
解答 解:∵AB∥CD,
∴∠A+∠ACD=180°,∠AEC=∠ECD,
∵∠A=80°,
∴∠ACD=100°,
∵CE平分∠ACD交AB于E,
∴∠ECD=$\frac{1}{2}∠ACD$=50°,
∴∠ECD=50°,
故答案为:50°.
点评 此题主要考查了平行线的性质,关键是掌握两直线平行,同旁内角互补,内错角相等.

练习册系列答案
相关题目
1.已知4个数据:-$\sqrt{2}$、2$\sqrt{2}$、a、b,其中a、b是方程x2-2x-1=0的两个根,则这4个数据的中位数是( )
| A. | 0.5 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
 如图,若三个小正方形的边长都为2,则图中阴影部分面积的和是$\frac{3π}{2}$.
如图,若三个小正方形的边长都为2,则图中阴影部分面积的和是$\frac{3π}{2}$.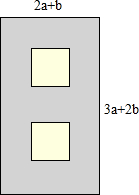 如图,在一块长为3a+2b,宽为2a+b的长方形木板中挖去两个边长为a+b的正方形,形成如图所示的“日”字形边框.
如图,在一块长为3a+2b,宽为2a+b的长方形木板中挖去两个边长为a+b的正方形,形成如图所示的“日”字形边框.