题目内容
11.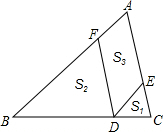 如图,D为△ABC的边BC上的一点,DE∥AB,DF∥AC,分别交AC,AB于点E,F,设△CDE,△BDF,四边形DEAF的面积分别为S1,S2,S3,求证:S3=2$\sqrt{{S}_{1}{S}_{2}}$.
如图,D为△ABC的边BC上的一点,DE∥AB,DF∥AC,分别交AC,AB于点E,F,设△CDE,△BDF,四边形DEAF的面积分别为S1,S2,S3,求证:S3=2$\sqrt{{S}_{1}{S}_{2}}$.
分析 设BF=a,AF=b,DE与AB间的距离为h,根据已知条件得到四边形AFDE是平行四边形,∠CED=∠A=∠BFD,∠B=∠EDC,推出△CDE∽△DBF,AF=DE,根据相似三角形的性质得到$\frac{{S}_{1}}{{S}_{2}}$=($\frac{DE}{BF}$)2=$\frac{{b}^{2}}{{a}^{2}}$,由三角形的面积公式得到S2=$\frac{1}{2}$ah,求出S1=$\frac{{b}^{2}h}{2a}$,得到S1S2=$\frac{{b}^{2}{h}^{2}}{4}$,由平行四边形的面积公式得到S3=bh,于是得到结论.
解答 证明:设BF=a,AF=b,DE与AB间的距离为h,
∵DE∥AB,DF∥AC,
∴四边形AFDE是平行四边形,∠CED=∠A=∠BFD,∠B=∠EDC,
∴△CDE∽△DBF,AF=DE,
∴$\frac{{S}_{1}}{{S}_{2}}$=($\frac{DE}{BF}$)2=$\frac{{b}^{2}}{{a}^{2}}$,
∵S2=$\frac{1}{2}$ah,
∴S1=$\frac{{b}^{2}h}{2a}$,
∴S1S2=$\frac{{b}^{2}{h}^{2}}{4}$,
∴bh=2$\sqrt{{S}_{1}{S}_{2}}$,
∵S3=bh,
∴S3=2$\sqrt{{S}_{1}{S}_{2}}$.
点评 本题考查了平行四边形、三角形的面积公式,平行四边形的判定和性质、相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
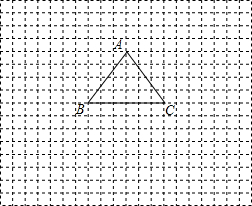 如图,等腰三角形ABC中AB=AC=5,BC=6.
如图,等腰三角形ABC中AB=AC=5,BC=6.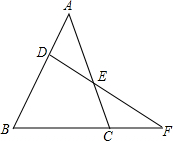 已知:如图△ABC中,D,E分别是AB,AC上的点,DE,BC的延长线相交于F,AD=CF,求证:$\frac{BC}{AB}$=$\frac{DE}{EF}$.
已知:如图△ABC中,D,E分别是AB,AC上的点,DE,BC的延长线相交于F,AD=CF,求证:$\frac{BC}{AB}$=$\frac{DE}{EF}$. 如图,已知AB:AD=AD:AE=BC:DE,试说明AD•CE=BD•AE.
如图,已知AB:AD=AD:AE=BC:DE,试说明AD•CE=BD•AE.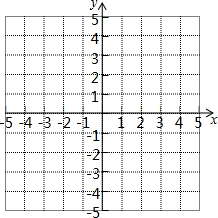 已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、
已知在平面直角坐标系中有三点A(-2,1)、B(3,1)、