题目内容
把一个矩形的硬纸片剪去一个正方形,若剩下的矩形与原矩形相似,求原矩形与新矩形相似比.
考点:相似多边形的性质
专题:
分析:根据相似多边形对应边的比等于相似比,设出原来矩形的长和宽,就可得到关于长、宽的方程,从而可以求解.
解答: 解:根据相似多边形对应边成比例,得
解:根据相似多边形对应边成比例,得
=
,
设原矩形ABCD的长AD=x,宽AB=y,则AE=x-y.
所以
=
,
解得:x=
y,或x=
(舍去).
所以
=
.
即原矩形与新矩形相似比是
.
 解:根据相似多边形对应边成比例,得
解:根据相似多边形对应边成比例,得| AB |
| AE |
| AD |
| AB |
设原矩形ABCD的长AD=x,宽AB=y,则AE=x-y.
所以
| y |
| x-y |
| x |
| y |
解得:x=
1+
| ||
| 2 |
1-
| ||
| 2 |
所以
| x |
| y |
1+
| ||
| 2 |
即原矩形与新矩形相似比是
1+
| ||
| 2 |
点评:本题考查了相似多边形的性质,根据相似得到方程,从而把几何问题转化为方程问题解决,解方程是解决本题的关键.

练习册系列答案
相关题目
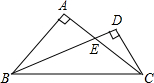 如图,在△ABC中,AB=AC,∠A=90°,BE是角平分线,CD⊥BE交BE的延长线于点D,求证:BE=2CD.
如图,在△ABC中,AB=AC,∠A=90°,BE是角平分线,CD⊥BE交BE的延长线于点D,求证:BE=2CD. 如图,一只密封的长方体盒子,长、宽、高分别是5cm、4cm、3cm.现在一只蚂蚁由A点出发去G点觅食,求这只蚂蚁从A点爬行到G的最短路短是路程.
如图,一只密封的长方体盒子,长、宽、高分别是5cm、4cm、3cm.现在一只蚂蚁由A点出发去G点觅食,求这只蚂蚁从A点爬行到G的最短路短是路程. 如图,AB∥CD,E为AD上一点,且BE、CE分别平分∠ABC、∠BCD,求证:AE=ED.
如图,AB∥CD,E为AD上一点,且BE、CE分别平分∠ABC、∠BCD,求证:AE=ED. 如图,在△ABC中,AB>AC,AD平分∠BAC交BC于D,求证:AB-AC>BD-CD.
如图,在△ABC中,AB>AC,AD平分∠BAC交BC于D,求证:AB-AC>BD-CD.