Question

20．在△ABC中，AB=AC=1，BC边上有2016个不同的点P₁，P₂，…，P₂₀₁₆，记m_i=AP_i²+BP_i•P_iC（i=1，2，…，2016），则m₁+m₂+…+m₂₀₁₆=2016．

Answer 1

分析 利用勾股定理求出AP_i²=AD²+P_iD²，进一步推出AP_i²+BP_i•P_iC=1，解答即可．

解答 解：如图所示：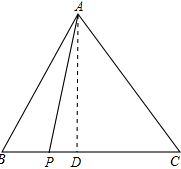
∵AP_i²=AD²+P_iD²
=AD²+（BD-BP_i）²
=AD²+BD²-2BD•BP_i+BP_i²
=1+BP_i（BP_i-BC）
=1-BP_i•P_iC，
∴AP_i²+BP_i•P_iC=1，
∴m₁+m₂+…+m₂₀₁₆=2016，
故答案为：2016．

点评 本题考查了勾股定理、等腰三角形的性质，根据题意，求出AP_i²+BP_i•P_iC=1是解题的关键．