题目内容
7.解不等式组$\left\{\begin{array}{l}{3x-1≤2(x+1)}\\{\frac{x-3}{2}<x-1}\end{array}\right.$.分析 先解出不等式组的各个不等式x的取值范围,然后求出x的公共部分,该公共部分就是不等式的解.
解答 解:$\left\{\begin{array}{l}{3x-1≤2(x+1)①}\\{\frac{x-3}{2}<x-1②}\end{array}\right.$
解不等式①,得x≤3.?
解不等式②,得x>-1;
∴原不等式组的解集为-1<x≤3.
点评 本题主要考查解一元一次不等式组,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
16.(-2)×(-$\frac{1}{2}$)的值是( )
| A. | 1 | B. | -1 | C. | 4 | D. | $-\frac{1}{4}$ |
17.一元一次不等式2x-3≥-1的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
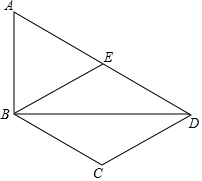 如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.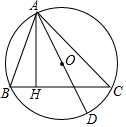 如图,AD是△ABC的外接圆O的直径,AH⊥BC于H.
如图,AD是△ABC的外接圆O的直径,AH⊥BC于H.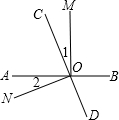 如图,直线AB、CD相交于点O,OM⊥AB.
如图,直线AB、CD相交于点O,OM⊥AB.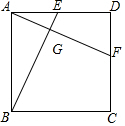 如图,正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接BE、AF,相交于G.求证:AF⊥BE.
如图,正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接BE、AF,相交于G.求证:AF⊥BE.