题目内容
已知矩形ABCD如图1放置,将矩形折叠,使B落在边AD(含端点)上,落点记为B′,折痕与线段AB交于E,与边BC或者边CD(含端点)交于F,则以E、B、B′为顶点的三角形△BB′E称为矩形ABCD的“折叠三角形”.
(1)由折叠三角形定义可知,矩形ABCD的任意一个折叠△BEB′都是一个 三角形.
(2)在矩形ABCD中,AB=6,AD=10,当F与点C重合时,在图2中画出这个折叠△BEB′,试求点B′的坐标并求这个折叠△BEB′的面积.

(1)由折叠三角形定义可知,矩形ABCD的任意一个折叠△BEB′都是一个
(2)在矩形ABCD中,AB=6,AD=10,当F与点C重合时,在图2中画出这个折叠△BEB′,试求点B′的坐标并求这个折叠△BEB′的面积.
考点:翻折变换(折叠问题),坐标与图形性质,勾股定理,矩形的性质
专题:
分析:(1)由折叠的性质即可得出B′E=BE,进而得出答案;
(2)由折叠性质可知,BC=B′C′=10,又DC=AB=6,即可求出DB′的长,以及AB′的长,再利用Rt△AB′E中,AE2+AB′2=BE′2,求出BE即可得出点B′的坐标并求这个折叠△BEB′的面积.
(2)由折叠性质可知,BC=B′C′=10,又DC=AB=6,即可求出DB′的长,以及AB′的长,再利用Rt△AB′E中,AE2+AB′2=BE′2,求出BE即可得出点B′的坐标并求这个折叠△BEB′的面积.
解答: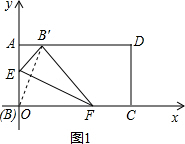 解:(1)如图1,∵将矩形折叠,使B落在边AD(含端点)上,落点记为B′,
解:(1)如图1,∵将矩形折叠,使B落在边AD(含端点)上,落点记为B′,
∴B′E=BE,
∴△BEB′是等腰三角形,
即由折叠三角形定义可知,矩形ABCD的任意一个折叠△BEB′都是一个等腰三角形;
故答案为:等腰;
(2)如图2,由题意可知,当点F与点C重合时,
由折叠性质可知,BC=B′C′=10,又DC=AB=6,
∴DB′=
=8,
∴AB′=2,
设BE=EB′=x,AE=6-x,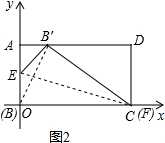
在Rt△AB′E中,
AE2+AB′2=BE′2,
∴(6-x)2+22=x2,
解得:x=
,
∴S△B′BE=
×BE×AB′=
×
×2=
,
故B′点坐标为(2,6).
 解:(1)如图1,∵将矩形折叠,使B落在边AD(含端点)上,落点记为B′,
解:(1)如图1,∵将矩形折叠,使B落在边AD(含端点)上,落点记为B′,∴B′E=BE,
∴△BEB′是等腰三角形,
即由折叠三角形定义可知,矩形ABCD的任意一个折叠△BEB′都是一个等腰三角形;
故答案为:等腰;
(2)如图2,由题意可知,当点F与点C重合时,
由折叠性质可知,BC=B′C′=10,又DC=AB=6,
∴DB′=
| 102-62 |
∴AB′=2,
设BE=EB′=x,AE=6-x,

在Rt△AB′E中,
AE2+AB′2=BE′2,
∴(6-x)2+22=x2,
解得:x=
| 10 |
| 3 |
∴S△B′BE=
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 3 |
| 10 |
| 3 |
故B′点坐标为(2,6).
点评:本题考查了图形的翻折变换以及到矩形的性质和三角形面积求法,利用数形结合的思想进行分析得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知△ABC的三边长为5cm,12cm,13cm,D、E、F分别是三边的中点,则△DEF的面积为( )
| A、30cm2 |
| B、15cm2 |
| C、7.5cm2 |
| D、3.75cm2 |
下列说法正确的是( )
| A、矩形的对角线互相垂直 |
| B、正方形的对角线相等且互相平分 |
| C、菱形的对角线相等 |
| D、等腰梯形的对角线互相平分 |
 如图,菱形ABCD的周长为24,DE⊥AB,垂足为E,DE:AD=
如图,菱形ABCD的周长为24,DE⊥AB,垂足为E,DE:AD= 如图,在△ABC中,D、E分别为AB、AC上的中点,F,G分别为BD、CE上的中点,已知BC=8cm,则FG=
如图,在△ABC中,D、E分别为AB、AC上的中点,F,G分别为BD、CE上的中点,已知BC=8cm,则FG=
 如图,C是
如图,C是