题目内容
14. 如图,四边形ABEG、GEFH、HFCD都是边长为a的正方形,△AEF与△CEA相似吗?为什么?
如图,四边形ABEG、GEFH、HFCD都是边长为a的正方形,△AEF与△CEA相似吗?为什么?
分析 由勾股定理求出AE,求出$\frac{AE}{EF}=\frac{EC}{AE}$,再由公共角∠AEF=∠CEA,即可得出△FEA∽△AEC.
解答 解:△AEF与△CEA相似;理由如下:
由勾股定理得:AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{2}$a,
∴$\frac{AE}{EF}=\frac{\sqrt{2}a}{a}$=$\sqrt{2}$,$\frac{EC}{AE}=\frac{2a}{\sqrt{2}a}$=$\sqrt{2}$,
∴$\frac{AE}{EF}=\frac{EC}{AE}$,
又∵∠AEF=∠CEA,
∴△AEF∽△CEA.
点评 本题考查了正方形的性质、勾股定理、相似三角形的判定;熟练掌握正方形的性质和相似三角形的判定方法,证明两边成比例是解决问题的关键.

练习册系列答案
相关题目
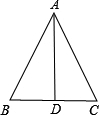 如图所示,已知∠B=∠C,点D为BC的中点,试说明AD平分∠BAC.
如图所示,已知∠B=∠C,点D为BC的中点,试说明AD平分∠BAC.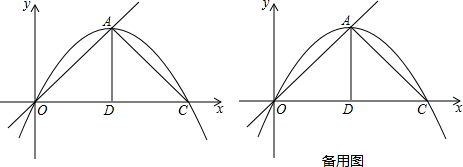
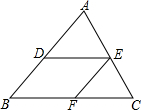 如图,DE∥BC,EF∥AB,则:
如图,DE∥BC,EF∥AB,则: