题目内容
15.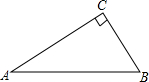 如图,在Rt△ABC中,∠ACB=90°,若AC=4,AB=5,则下列结论正确的是( )
如图,在Rt△ABC中,∠ACB=90°,若AC=4,AB=5,则下列结论正确的是( )| A. | sinA=$\frac{3}{4}$ | B. | tanA=$\frac{3}{4}$ | C. | tanA=$\frac{4}{3}$ | D. | cosA=$\frac{3}{5}$ |
分析 先利用勾股定理计算出BC=3,然后根据锐角三角函数的定义求出∠A的三角函数值,再对各选项进行判断.
解答 解:∵∠ACB=90°,AC=4,AB=5,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=3,、
∴sinA=$\frac{BC}{AB}$=$\frac{3}{5}$,cosA=$\frac{AC}{AB}$=$\frac{4}{5}$,tanA=$\frac{BC}{AC}$=$\frac{3}{4}$.
故选B.
点评 本题考查了锐角三角函数的定义:在Rt△ABC中,锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA;锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA;锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
6.下列属于准确数的是( )
| A. | 我国有13亿人口 | B. | 你的身高是1.63m | ||
| C. | 我国人口的平均寿命为74岁 | D. | 七年三班有50名学生 |