题目内容
7.已知A、B、C三点在同一条直线上,M、N分别为线段AB、BC的中点,且AB=60,BC=40,求MN的长.分析 此题首先要考虑A、B、C三点在直线上的不同位置:点C在线段AB上或点C在线段AB的延长线上.再根据线段中点的概念进行计算.
解答  解:(1)当当C在线段AB上时,
解:(1)当当C在线段AB上时,
∵M、N分别为AB、BC的中点,
∴BM=$\frac{1}{2}$AB=30,BN=$\frac{1}{2}$BC=20;
∴MN=50;
(2)当C在线段AB延长线上时,同理可知BM=30,BN=20,
∴MN=10;
所以MN=50或10.
点评 本题考查了两点间的距离,利用线段中点的性质得出BM,BN的长,利用线段的和差得出MN的长,分类讨论是解题关键.

练习册系列答案
相关题目
15.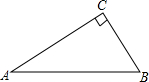 如图,在Rt△ABC中,∠ACB=90°,若AC=4,AB=5,则下列结论正确的是( )
如图,在Rt△ABC中,∠ACB=90°,若AC=4,AB=5,则下列结论正确的是( )
 如图,在Rt△ABC中,∠ACB=90°,若AC=4,AB=5,则下列结论正确的是( )
如图,在Rt△ABC中,∠ACB=90°,若AC=4,AB=5,则下列结论正确的是( )| A. | sinA=$\frac{3}{4}$ | B. | tanA=$\frac{3}{4}$ | C. | tanA=$\frac{4}{3}$ | D. | cosA=$\frac{3}{5}$ |
2.-$\frac{1}{2003}$的倒数为( )
| A. | $\frac{1}{2003}$ | B. | -$\frac{1}{2003}$ | C. | 2013 | D. | -2013 |
19.下列实数中是无理数的是( )
| A. | $\sqrt{4}$ | B. | π | C. | 0.$\stackrel{•}{3}$$\stackrel{•}{8}$ | D. | -$\frac{22}{7}$ |
16.某地要把248吨物资从某地运往甲、乙两地,用大、小两种货车共20辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围).
(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
| 运往地车型 | 甲地(元/辆) | 乙地(元/辆) |
| 大货车 | 620 | 700 |
| 小货车 | 400 | 550 |
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围).
(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
17.下面所给的交通标志是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
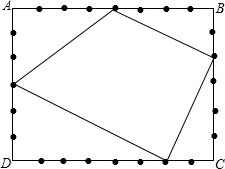 如图,矩形ABCD中,AB=8,AD=6,四边上各取一个整点(即到边的端点距离为正整数的点),并且由这4个点为顶点的四边形的面积为25,那么这样的4个点共有7种不同的取法.
如图,矩形ABCD中,AB=8,AD=6,四边上各取一个整点(即到边的端点距离为正整数的点),并且由这4个点为顶点的四边形的面积为25,那么这样的4个点共有7种不同的取法.