题目内容
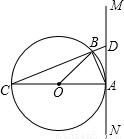
 如图,⊙O的直径AC为10cm,弦AB为6cm,∠ABC的平分线交⊙O于D,求:
如图,⊙O的直径AC为10cm,弦AB为6cm,∠ABC的平分线交⊙O于D,求:(1)弦BC的长;
(2)四边形ABCD的面积.
分析:(1)根据圆周角定理即可推出∠ABC=90°,由AC为10cm,弦AB为6cm,根据勾股定理即可推出BC=8cm;
(2)由BD平分∠ABC,求出∠ABD=∠CBD=45°,即可确定DA=DC,然后根据特殊角的三角函数值即可求出DA=DC=5
,根据三角形的面积公式求出△ABC和△ADC的面积后,结合图形即可求出结论.
(2)由BD平分∠ABC,求出∠ABD=∠CBD=45°,即可确定DA=DC,然后根据特殊角的三角函数值即可求出DA=DC=5
| 2 |
解答:解:(1)∵AC为⊙O的直径,
∴∠ABC=90°,
又∵AC=10cm,AB=6cm,
∴BC=8cm;
(2)∵BD平分∠ABC,
∴∠ABD=∠CBD=45°,
∴DA=DC,
∵∠ADC=90°,AC=10cm,
∴DA=DC=5
cm,
∵BC=8cm,AB=6cm,
∴S△ABC=
=24cm2,S△ADC=
=25cm2,
∴S四边形ABCD=24+25=49cm2.
∴∠ABC=90°,
又∵AC=10cm,AB=6cm,
∴BC=8cm;
(2)∵BD平分∠ABC,
∴∠ABD=∠CBD=45°,
∴DA=DC,
∵∠ADC=90°,AC=10cm,
∴DA=DC=5
| 2 |
∵BC=8cm,AB=6cm,
∴S△ABC=
| BA•BC |
| 2 |
| DA•DC |
| 2 |
∴S四边形ABCD=24+25=49cm2.
点评:本题主要考查圆周角定理,三角形面积公式,勾股定理等知识点,关键在于运用数形结合的思想推出BC,CA,DC的长.

练习册系列答案
相关题目
 如图,⊙O的直径AC=2,∠BAD=75°,∠ACD=45°,则四边形ABCD的周长为
如图,⊙O的直径AC=2,∠BAD=75°,∠ACD=45°,则四边形ABCD的周长为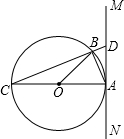 如图,⊙O的直径AC=13,弦BC=12.过点A作直线MN,使∠BAM=
如图,⊙O的直径AC=13,弦BC=12.过点A作直线MN,使∠BAM=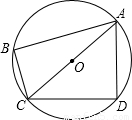
 ∠AOB.
∠AOB.