题目内容
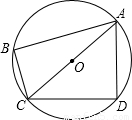
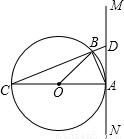
如图,⊙O的直径AC=13,弦BC=12.过点A作直线MN,使∠BAM= ∠AOB.
∠AOB.(1)求证:MN是⊙O的切线;
(2)延长CB交MN于点D,求AD的长.
【答案】分析:(1)证MN⊥AC即可.由AC是直径得∠ABC=90°,从而有∠C+∠BAC=90°;因∠BAM= ∠AOB=∠C,所以∠BAM+∠BAC=90°,得证;
∠AOB=∠C,所以∠BAM+∠BAC=90°,得证;
(2)根据勾股定理可求AB的长.由tanC= =
= 可求AD.
可求AD.
解答:(1)证明:∵AC是直径,
∴∠ABC=90°,∠C+∠BAC=90°.
∵∠BAM= ∠AOB=∠C,
∠AOB=∠C,
∴∠BAM+∠BAC=90°,即∠CAM=90°.
∴MN是⊙O的切线.
(2)解:∵∠ABC=90°,AC=13,BC=12,
∴AB=5.
∵tanC= =
= ,
,
∴ ,
,
∴AD= .
.
点评:此题考查了切线的判定、解直角三角形等知识点,难度中等.
 ∠AOB=∠C,所以∠BAM+∠BAC=90°,得证;
∠AOB=∠C,所以∠BAM+∠BAC=90°,得证;(2)根据勾股定理可求AB的长.由tanC=
 =
= 可求AD.
可求AD.解答:(1)证明:∵AC是直径,
∴∠ABC=90°,∠C+∠BAC=90°.
∵∠BAM=
 ∠AOB=∠C,
∠AOB=∠C,∴∠BAM+∠BAC=90°,即∠CAM=90°.
∴MN是⊙O的切线.
(2)解:∵∠ABC=90°,AC=13,BC=12,
∴AB=5.
∵tanC=
 =
= ,
,∴
 ,
,∴AD=
 .
.点评:此题考查了切线的判定、解直角三角形等知识点,难度中等.

练习册系列答案
相关题目
 如图,⊙O的直径AC=2,∠BAD=75°,∠ACD=45°,则四边形ABCD的周长为
如图,⊙O的直径AC=2,∠BAD=75°,∠ACD=45°,则四边形ABCD的周长为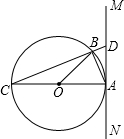 如图,⊙O的直径AC=13,弦BC=12.过点A作直线MN,使∠BAM=
如图,⊙O的直径AC=13,弦BC=12.过点A作直线MN,使∠BAM= 如图,⊙O的直径AC为10cm,弦AB为6cm,∠ABC的平分线交⊙O于D,求:
如图,⊙O的直径AC为10cm,弦AB为6cm,∠ABC的平分线交⊙O于D,求: