题目内容
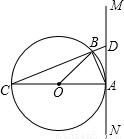
 如图,⊙O的直径AC=2,∠BAD=75°,∠ACD=45°,则四边形ABCD的周长为
如图,⊙O的直径AC=2,∠BAD=75°,∠ACD=45°,则四边形ABCD的周长为分析:根据圆周角定理可证∠D=90°,∠ACD=45°,∠BAC=30°,∠B=90°,即可分别求出AD=CD=AC•sin45°=2×
=
,AB=AC•cos30°=2×
=
,BC=AC•sin30°=2×
=1,即可求四边形ABCD的周长.
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
解答:解:∵⊙O的直径,AC=2,∠BAD=75°,∠ACD=45°,
∴∠D=90°,∠ACD=45°,∠BAC=30°,∠B=90°.
∴AD=CD=AC•sin45°=2×
=
,
AB=AC•cos30°=2×
=
,
BC=AC•sin30°=2×
=1,
∴四边形ABCD的周长=AD+CD+BC+AB=1+2
+
.
∴∠D=90°,∠ACD=45°,∠BAC=30°,∠B=90°.
∴AD=CD=AC•sin45°=2×
| ||
| 2 |
| 2 |
AB=AC•cos30°=2×
| ||
| 2 |
| 3 |
BC=AC•sin30°=2×
| 1 |
| 2 |
∴四边形ABCD的周长=AD+CD+BC+AB=1+2
| 2 |
| 3 |
点评:本题重点考查了同弧所对的圆周角相等、直径所对的圆周角为直角及解直角三角形的知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
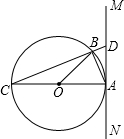 如图,⊙O的直径AC=13,弦BC=12.过点A作直线MN,使∠BAM=
如图,⊙O的直径AC=13,弦BC=12.过点A作直线MN,使∠BAM= 如图,⊙O的直径AC为10cm,弦AB为6cm,∠ABC的平分线交⊙O于D,求:
如图,⊙O的直径AC为10cm,弦AB为6cm,∠ABC的平分线交⊙O于D,求: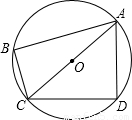
 ∠AOB.
∠AOB.