题目内容
16.下列各式中,正确的是( )| A. | (-1)0=-1 | B. | (-1)-1=1 | ||
| C. | (x-y)-2=-(y-x)2(x≠y) | D. | x-n=$(\frac{1}{x})$n(x≠0,n为自然数) |
分析 分别根据0指数幂及负整数指数幂的运算法则对各选项进行逐一计算即可.
解答 解:A、(-1)0=1≠-1,故本选项错误;
B、(-1)-1=$\frac{1}{-1}$=-1≠1,故本选项错误;
C、(x-y)-2=$\frac{1}{(x-y)^{2}}$≠-(y-x)2,故本选项错误;
D、x-n=$\frac{1}{{x}^{n}}$=$(\frac{1}{x})$n,故本选项正确.
故选D.
点评 本题考查的是负整数指数幂,熟知非0数的负整数指数幂等于该数正整数指数幂的倒数是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若x>0,y>0,则化简x$\sqrt{xy}$÷y$\sqrt{\frac{x}{y}}$×$\sqrt{\frac{y}{x}}$等于( )
| A. | $\frac{y}{x}$$\sqrt{xy}$ | B. | $\frac{x}{y}$$\sqrt{xy}$ | C. | $\sqrt{xy}$ | D. | xy$\sqrt{xy}$ |
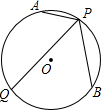 如图,点A、B是⊙O上的定点,且圆周角∠APB=120°,∠APB的角平分线交⊙O于点Q.(1)当点P在$\widehat{AB}$上运动(不与点A、B重合)时,问点Q移动吗?试说明理由.
如图,点A、B是⊙O上的定点,且圆周角∠APB=120°,∠APB的角平分线交⊙O于点Q.(1)当点P在$\widehat{AB}$上运动(不与点A、B重合)时,问点Q移动吗?试说明理由.