题目内容
13．已知关于 x 的一元二次方程 ax2+bx+c=0，若 a-b+c=0，则方程有一个根是（ ）| A． | 1 | B． | -1 | C． | 2 | D． | -2 |
分析 将x=-1代入方程ax2+bx+c=0中的左边，得到a-b+c，由a-b+c=0得到方程左右两边相等，即x=-1是方程的解．
解答 解：将x=-1代入ax2+bx+c=0的左边得：a×（-1）2+b×（-1）+c=a-b+c，
∵a-b+c=0，
∴x=-1是方程ax2+bx+c=0的根．
即方程的一个根为x=-1．
故选B．
点评 此题考查了一元二次方程的解的意义：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．掌握定义是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．下列数中，最小的数的选项是（ ）
| A． | 3 | B． | |-2| | C． | （-1）3 | D． | 4的相反数 |
4．2016年5月下旬，中国大数据博览会在贵阳举行，参加此次大会的人数约有89000人，将89000用科学记数法表示为（ ）
| A． | 89×103 | B． | 8.9×103 | C． | 8.9×104 | D． | 0.89×105 |
1．下列说法中正确的是（ ）
| A． | 9的平方根为3 | B． | $\frac{1}{\sqrt{2}}$化简后的结果是$\frac{\sqrt{2}}{2}$ | ||
| C． | $\sqrt{8}$最简二次根式 | D． | -27没有立方根 |
18．化简$\frac{{x}^{2}-25}{{x}^{2}-5x}$-1结果正确的是（ ）
| A． | $\frac{5}{x}$ | B． | $\frac{x-5}{x}$ | C． | $\frac{x+5}{x}$ | D． | $\frac{x}{x-5}$ |
5．
如图，?ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=$\frac{1}{2}$BC，连接OE．下列结论：
①OB=AB； ②OE=$\frac{1}{4}$BC；③S?ABCD=AB•AC； ④∠CAD=30°．
其中正确结论的个数是（ ）
如图，?ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=$\frac{1}{2}$BC，连接OE．下列结论：①OB=AB； ②OE=$\frac{1}{4}$BC；③S?ABCD=AB•AC； ④∠CAD=30°．
其中正确结论的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
2．关于x的方程$\frac{3x-2}{x+2}$=2+$\frac{m}{x+2}$无解，则m的值为（ ）
| A． | -5 | B． | 5 | C． | -2 | D． | -8 |
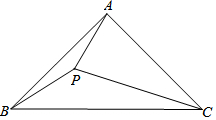已知，如图，在△ABC中，AB=AC，∠BAC=α，且60°＜α＜120°，P是△ABC内部一点，且PC=AC，∠PCA=120°-α．