题目内容
5. 如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:
如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:①OB=AB; ②OE=$\frac{1}{4}$BC;③S?ABCD=AB•AC; ④∠CAD=30°.
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由?ABCD中,∠ADC=60°,易得△ABE是等边三角形,又由AB=$\frac{1}{2}$BC,证得∠CAD=30°;继而证得AC⊥AB,得②S?ABCD=AB•AC;可得OE是三角形的中位线,证得OE=$\frac{1}{4}$BC;即可得出结论.
解答 解:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB=$\frac{1}{2}$BC,
∴AE=$\frac{1}{2}$BC,
∴∠BAC=90°,
∴∠CAD=30°,故④正确;
∵AC⊥AB,
∴S?ABCD=AB•AC,故③正确,
∵AB=$\frac{1}{2}$BC,OB=$\frac{1}{2}$BD,
∵BD>BC,
∴AB≠OB,故①错误;
∵∠CAD=30°,∠AEB=60°,AD∥BC,
∴∠EAC=∠ACE=30°,
∴AE=CE,
∴BE=CE,∵OA=OC,
∴OE=$\frac{1}{2}$AB,
∵AB=$\frac{1}{2}$BC,
∴OE=$\frac{1}{4}$BC.故②正确.
故选:C.
点评 此题考查了平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质.注意证得△ABE是等边三角形,OE是△ABC的中位线是关键.

练习册系列答案
相关题目
15.已知反比例函数y=$\frac{k}{x}$的图象经过点P(-1,2),则这个函数的图象位于( )
| A. | 第一、三象限 | B. | 第二、三象限 | C. | 第二、四象限 | D. | 第三、四象限 |
16.当a=1时,a-3的值为( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
13.已知关于 x 的一元二次方程 ax2+bx+c=0,若 a-b+c=0,则方程有一个根是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
20.“a的$\frac{1}{2}$与b的3倍的差”用代数式表示是( )
| A. | 3($\frac{1}{2}$a-b) | B. | $\frac{1}{2}$a-3b | C. | 3(a-$\frac{1}{2}$b) | D. | (a-$\frac{1}{2}$)-3b |
10.计算(a3b2)3÷(-a3)2的结果是( )
| A. | a6b2 | B. | a2b5 | C. | a5b3 | D. | a3b6 |
17.根据表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断该二次函数的图象与x轴( )
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | 4 | -0.5 | -2 | -0.5 | … |
| A. | 只有一个交点 | B. | 有两个交点,且它们分别在y轴两侧 | ||
| C. | 有两个交点,且它们均在y轴同侧 | D. | 无交点 |
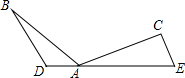 如图,点A为线段DE上一点,AB=AC=$\sqrt{7}$,∠D=∠BAC=2∠E=120°,若AE-BD=BD-CE=1cm,则△ACE的面积=$\frac{3\sqrt{3}}{4}$cm2.
如图,点A为线段DE上一点,AB=AC=$\sqrt{7}$,∠D=∠BAC=2∠E=120°,若AE-BD=BD-CE=1cm,则△ACE的面积=$\frac{3\sqrt{3}}{4}$cm2.