题目内容
已知数a，b，c 在数轴上的对应点如图所示，化简 b+|a+b|-|-c|-|b-c|=________．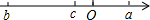
b-a
分析：由数轴上点的位置，利用数轴上右边的数总比左边的数大，判断出a，b及c的大小，且利用绝对值表示在数轴上到原点的距离，判断出|a|，|b|，|c|的大小，进而利用绝对值的代数意义化简所求的式子，去括号合并后即可得到结果．
解答：由数轴上点的位置可得：b＜c＜0＜a，且|c|＜|a|＜|b|，
∴a+b＜0，b-c＜0，
∴b+|a+b|-|-c|-|b-c|=b-（a+b）-（-c）-[-（b-c）]=b-a-b+c+b-c=b-a．
故答案为：b-a
点评：此考查了整式的加减运算，涉及的知识有：绝对值的代数意义，数轴，去括号法则，以及合并同类项法则，其中判断出绝对值号里式子的正负是解本题的关键．
分析：由数轴上点的位置，利用数轴上右边的数总比左边的数大，判断出a，b及c的大小，且利用绝对值表示在数轴上到原点的距离，判断出|a|，|b|，|c|的大小，进而利用绝对值的代数意义化简所求的式子，去括号合并后即可得到结果．
解答：由数轴上点的位置可得：b＜c＜0＜a，且|c|＜|a|＜|b|，
∴a+b＜0，b-c＜0，
∴b+|a+b|-|-c|-|b-c|=b-（a+b）-（-c）-[-（b-c）]=b-a-b+c+b-c=b-a．
故答案为：b-a
点评：此考查了整式的加减运算，涉及的知识有：绝对值的代数意义，数轴，去括号法则，以及合并同类项法则，其中判断出绝对值号里式子的正负是解本题的关键．
练习册系列答案
状元坊全程突破导练测系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
已知数a、b、c在数轴上的位置如图所示，化简|b+c|+|c-a|-|b-a|．
已知数a、b、c在数轴上的位置如图所示，试化简|a-c|-|a+b+c|-|b-a|+|b+c|=
（1）已知数a，b，c在数轴上对应的点如图所示，化简：|a|-|b-a|+|c+a|-|a+b|．
已知数a，b表示的点在数轴上的位置如图所示．