题目内容
12.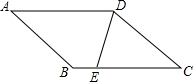 已知:如图,AD∥BC,∠A=∠C.
已知:如图,AD∥BC,∠A=∠C.(1)求证:AB∥CD;
(2)若DE平分∠ADC交BC于E,∠A=40°,求∠DEC的度数.
分析 (1)根据平行线的性质得出∠A+∠B=180°,求出∠C+∠B=180°,根据平行线的判定得出即可.
(2)根据平行线的性质得出∠A+∠ADC=180°,求出∠ADC=140°,根据角平分线定义得出∠ADE=$\frac{1}{2}$∠ADC=70°,根据平行线的性质得出即可.
解答 (1)证明:∵AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠C,
∴∠C+∠B=180°,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠A+∠ADC=180°,
∵∠A=40°,
∴∠ADC=140°,
∵DE平分∠ADC,
∴∠ADE=$\frac{1}{2}$∠ADC=70°,
∵AD∥BC,
∴∠DEC=∠ADE=70°.
点评 本题考查了平行线的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
2.甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别从A,B两端同时出发,分别到另一端点处掉头,掉头时间不计.甲、乙两人距A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200)如图所示.综合图象信息解答下列问题:
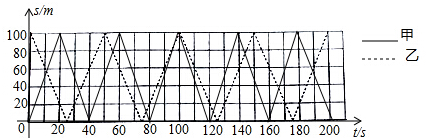
(1)求甲乙两人的速度;
(2)完成下列表格:
(3)在(2)的基础上,通过计算判断,当t=390s时,他们是否相遇?若相遇,应是第几次?并求出此时甲离A端的距离.

(1)求甲乙两人的速度;
(2)完成下列表格:
| 两人相遇次数(单位:次) | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和(单位:m) | 100 | 300 | 500 | 700 | … | 200n-100 |
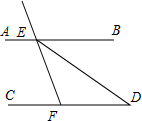 如图,若∠EFD=110°,∠FED=35°,ED平分∠BEF,那么AB与CD平行吗?请说明你的理由.
如图,若∠EFD=110°,∠FED=35°,ED平分∠BEF,那么AB与CD平行吗?请说明你的理由.