题目内容
16. 如图所示,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BF=CE.求证:AD平分∠BAC.
如图所示,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BF=CE.求证:AD平分∠BAC.
分析 根据垂直定义求出∠BFD=∠CED=90°,根据AAS推出△BFD≌△CED,根据全等三角形的性质推出DF=DE,根据角平分线性质求出即可.
解答 证明:∵BE⊥AC,CF⊥AB,
∴∠BFD=∠CED=90°,
在△BFD和△CED中
$\left\{\begin{array}{l}{∠BFD=∠CED}\\{∠BDF=∠CDE}\\{BF=CE}\end{array}\right.$
∴△BFD≌△CED(AAS),
∴DF=DE,
∵BE⊥AC,CF⊥AB,
∴AD平分∠BAC.
点评 本题考查了全等三角形的性质和判定,角平分线性质的应用,能推出DF=DE是解此题的关键,注意:全等三角形的判定定理有:SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等,角平分线上的点到角的两边的距离相等.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
8.某同学用一扇形纸片为玩偶制作了一个圆锥形帽子(不考虑接缝),已知扇形的半径为13cm,扇形的弧长为10π cm,那么这个圆锥形帽子的高是( )
| A. | 5cm | B. | 12cm | C. | 13cm | D. | 14cm |
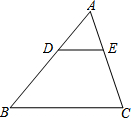 如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E.若$\frac{AD}{BD}$=$\frac{2}{3}$,DE=6,则BC的长为15.
如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E.若$\frac{AD}{BD}$=$\frac{2}{3}$,DE=6,则BC的长为15.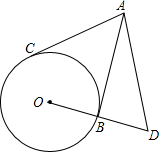 如图,AB、AC是⊙O的切线,切点分别为B、C,D是OB延长线上的一点,且BD=OB,∠DAC=69°,求∠ADO的度数.
如图,AB、AC是⊙O的切线,切点分别为B、C,D是OB延长线上的一点,且BD=OB,∠DAC=69°,求∠ADO的度数.