题目内容
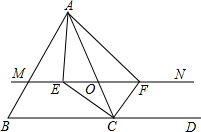 如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,∠ACB以及外角∠ACD的平分线分别交MN于点E、F.
如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,∠ACB以及外角∠ACD的平分线分别交MN于点E、F.(1)求证:OE=OF;
(2)当点O运动到AC边的什么位置时,四边形AECF是矩形?回答并证明你的结论.
考点:矩形的判定,等腰三角形的判定与性质
专题:
分析:(1)根据平行线性质和角平分线性质,由平行线所夹的内错角相等证得即可;
(2)当点O运动到AC的中点时,四边形AECF是矩形,根据矩形的判定方法,即一个角是直角的平行四边形是矩形可证.
(2)当点O运动到AC的中点时,四边形AECF是矩形,根据矩形的判定方法,即一个角是直角的平行四边形是矩形可证.
解答:证明(1)∵CE平分∠ACB,
∴∠ACE=∠BCE,
∵MN∥BC,
∴∠OEC=∠BCE,
∴∠ACE=∠OEC,
∴OE=OC,
同理OF=OC,
∴OE=OF;
(2)当点O运动到AC边的中点时,四边形AECF是矩形.
证明:∵O为AC中点,
∴OA=OC,
又∵OE=OF,
∴四边形AECF为平行四边形,
∵OE=OC,
∴2OE=2OC,
即AC=EF.
∴□AECF为矩形.
∴∠ACE=∠BCE,
∵MN∥BC,
∴∠OEC=∠BCE,
∴∠ACE=∠OEC,
∴OE=OC,
同理OF=OC,
∴OE=OF;
(2)当点O运动到AC边的中点时,四边形AECF是矩形.
证明:∵O为AC中点,
∴OA=OC,
又∵OE=OF,
∴四边形AECF为平行四边形,
∵OE=OC,
∴2OE=2OC,
即AC=EF.
∴□AECF为矩形.
点评:本题涉及矩形的判定定理,解答此类题的关键是要突破思维定势的障碍,运用发散思维,多方思考,探究问题在不同条件下的不同结论,挖掘它的内在联系,向“纵、横、深、广”拓展,从而寻找出添加的条件和所得的结论.

练习册系列答案
相关题目
平面直角坐标系内一点P(-6,5)关于原点对称点的坐标是( )
| A、(6,-5) |
| B、(-6,-5) |
| C、(5,-6) |
| D、(6,5) |
2015年1月1日,《深圳经济特区促进全民健条例》正式实施,小颖为了了解她所在小区(约有3000人)市民的运动健身情况,她应采用的收集数据的方式是( )
| A、对小区所有成年人发放问卷进行调查 |
| B、对小区内所有中小学生发放问卷进行调查 |
| C、在小区出入口对出入居民随机发放问卷进行调查 |
| D、挨家挨户发放问卷进行调查 |
 如图,直线AB、CD交EF于点G、H,∠2=∠3,∠1=70°,求∠4的度数.
如图,直线AB、CD交EF于点G、H,∠2=∠3,∠1=70°,求∠4的度数.