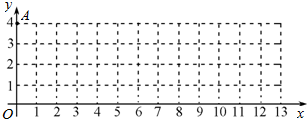
题目内容
点A（
，y1）、B（2，y2）、C（-
，y3）在抛物线y=2（x-1）2+k上，则y1、y2、y3的大小关系为 ．
| 2 |
| 5 |
考点：二次函数图象上点的坐标特征
专题：
分析：对二次函数y=3（x-1）2+k，对称轴x=1，则A、B、C的横坐标离对称轴越近，则纵坐标越小，由此判断y1、y2、y3的大小．
解答：解：在二次函数y=2（x-1）2+k，对称轴x=1，
在图象上的三点A（
，y1）、B（2，y2）、C（-
，y3），
|
-1|＜|2-1|＜|-
-1|，
则y1、y2、y3的大小关系为y1＜y2＜y3．
故答案为y1＜y2＜y3．
在图象上的三点A（
| 2 |
| 5 |
|
| 2 |
| 5 |
则y1、y2、y3的大小关系为y1＜y2＜y3．
故答案为y1＜y2＜y3．
点评：本题考查了二次函数图象上点的坐标特征，由点的横坐标到对称轴的距离判断点的纵坐标的大小．
练习册系列答案
相关题目
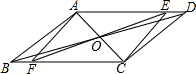如图，在?ABCD中，对角线AC、BD交于点O，并且∠DAC=60°，∠ADB=15°．点E是AD边上一动点，延长EO交BC于点F．当点E从D点向A点移动过程中（点E与点D，A不重合），则四边形AFCE的变化是（ ）| A、平行四边形→矩形→平行四边形→菱形→平行四边形 |
| B、平行四边形→菱形→平行四边形→矩形→平行四边形 |
| C、平行四边形→矩形→平行四边形→正方形→平行四边形 |
| D、平行四边形→矩形→菱形→正方形→平行四边形 |
如图，在Rt△ABC中，∠ACB=90°，CD垂直于AB，垂足为点D，DB=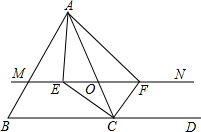
如图，在△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，∠ACB以及外角∠ACD的平分线分别交MN于点E、F．