题目内容
9.计算:$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$+$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$…$\sqrt{1+\frac{1}{201{3}^{2}}+\frac{1}{201{4}^{2}}}$.分析 观察几道算式可知,结果的分母为二次根式中两个分母的积,分子比分母大1,由此得出一般规律;将一般规律的结果变形,再将n的值代入寻找抵消规律.
解答 解:∵$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=$\frac{{n}^{2}+n+1}{n(n+1)}=1+\frac{1}{n}-\frac{1}{n+1}$,
∴原式=1+1-$\frac{1}{2}$+1+$\frac{1}{2}$$-\frac{1}{3}$+…+1$+\frac{1}{2013}-\frac{1}{2014}$=2013+1-$\frac{1}{2014}$=2013$\frac{2013}{2014}$.
点评 本题考查了二次根式的化简求值.关键是根据算式发现一般规律,运用一般规律代值计算,寻找算式的抵消规律.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
19.据统计,中国每年浪费的食物总量折合粮食约为50000000吨,将50000000用科学记数法表示为( )
| A. | 5×107 | B. | 50×106 | C. | 5×106 | D. | 0.5×108 |
20. 如图,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF,若∠BAF=80°,则∠C的度数为( )
如图,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF,若∠BAF=80°,则∠C的度数为( )
 如图,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF,若∠BAF=80°,则∠C的度数为( )
如图,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF,若∠BAF=80°,则∠C的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 80° |
17.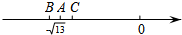 如图,在数轴上,点A表示的数是-$\sqrt{13}$,点B,C表示的数是两个连续的整数,则这两个整数为( )
如图,在数轴上,点A表示的数是-$\sqrt{13}$,点B,C表示的数是两个连续的整数,则这两个整数为( )
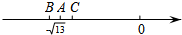 如图,在数轴上,点A表示的数是-$\sqrt{13}$,点B,C表示的数是两个连续的整数,则这两个整数为( )
如图,在数轴上,点A表示的数是-$\sqrt{13}$,点B,C表示的数是两个连续的整数,则这两个整数为( )| A. | 4和5 | B. | -5和-4 | C. | 3和4 | D. | -4和-3 |
14.-$\frac{1}{5}$的绝对值等于( )
| A. | 5 | B. | -5 | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
1. 如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
 如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
 如图,在一张长为5cm,宽为4cm的长方形纸片上,现要剪下一个腰长为3cm的等腰三角形(要求:等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上),则剪下的等腰三角形的底边的长为3$\sqrt{2}$,2$\sqrt{6}$,$\sqrt{30}$cm.
如图,在一张长为5cm,宽为4cm的长方形纸片上,现要剪下一个腰长为3cm的等腰三角形(要求:等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上),则剪下的等腰三角形的底边的长为3$\sqrt{2}$,2$\sqrt{6}$,$\sqrt{30}$cm.