题目内容
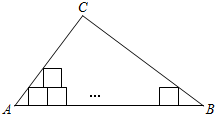 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.在△ABC内并排(不重叠)放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放( )个小正方形纸片.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.在△ABC内并排(不重叠)放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放( )个小正方形纸片.| A、14个 | B、15个 |
| C、16个 | D、17个 |
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:首先求得斜边上的高线的长度,即可确定小正方形的排数,然后确定每排的个数即可.
解答:解:作CF⊥AB于点F.

在Rt△ABC中,∠C=90°,AC=8,BC=6,则由勾股定理,得AB=10
∵S△ABC=
AB•CF=
AC•BC
∴CF=4.8.
则小正方形可以排4排.
最下边的一排小正方形的上边的边所在的直线与△ABC的边交于D、E.
∵DE∥AB,
=
,
=
,
解得:DE=
整数部分是7.
则最下边一排是7个正方形.
第二排正方形的上边的边所在的直线与△ABC的边交于G、H.
=
,
解得GH=
整数部分是5,
则第二排是5个正方形;
同理:第三排是:3个;
第四排是:1个.
则正方形的个数是:7+5+3+1=16.
故选:C.

在Rt△ABC中,∠C=90°,AC=8,BC=6,则由勾股定理,得AB=10
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CF=4.8.
则小正方形可以排4排.
最下边的一排小正方形的上边的边所在的直线与△ABC的边交于D、E.
∵DE∥AB,
| DE |
| AB |
| 4.8-1 |
| 4.8 |
| DE |
| AB |
| 3.8 |
| 4.8 |
解得:DE=
| 95 |
| 12 |
则最下边一排是7个正方形.
第二排正方形的上边的边所在的直线与△ABC的边交于G、H.
| GH |
| AB |
| 4.8-2 |
| 4.8 |
解得GH=
| 35 |
| 6 |
则第二排是5个正方形;
同理:第三排是:3个;
第四排是:1个.
则正方形的个数是:7+5+3+1=16.
故选:C.
点评:本题考查了相似三角形的判定与性质和正方形的性质,解题的关键是运用相似三角形的对应边上的比等于对应高的比.

练习册系列答案
相关题目
下面性质中,菱形不一定具有的是( )
| A、对角线相等 |
| B、是中心对称图形 |
| C、是轴对称图形 |
| D、对角线互相平分 |
已知x=2是关于x的方程x-2a=0的解,则a的值为( )
| A、4 | B、3 | C、1 | D、2 |
设A(x1,y1),B(x2,y2)是正比例函数y=-2x图象上的两点,若x1<x2<0,则y1与y2之间的关系是( )
| A、y2<y1<0 |
| B、y1<y2<0 |
| C、y2>y1>0 |
| D、y1>y2>0 |
由下列长度的三条线段组成三角形是直角三角形的是( )
| A、2,3,4 |
| B、3,4,5 |
| C、4,5,6 |
| D、6,7,8 |
 如图,?ABCD中,AB、BC长分别为12和24,边AD与BC之间的距离为5,则AB与CD间的距离为
如图,?ABCD中,AB、BC长分别为12和24,边AD与BC之间的距离为5,则AB与CD间的距离为