题目内容
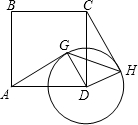 如图,在边长为4的正方形ABCD中,以D为圆心、2为半径画圆,点G是⊙D上任意一点,连接GD、AG.将GD绕点D按顺时针方向旋转90°,得到DH,连接CH、GH.
如图,在边长为4的正方形ABCD中,以D为圆心、2为半径画圆,点G是⊙D上任意一点,连接GD、AG.将GD绕点D按顺时针方向旋转90°,得到DH,连接CH、GH.(1)当CH与⊙D相切时,
①求证:AG与⊙D相切;
②求点H到CD的距离.
(2)请直接写出点B到CH的距离的最大值.
考点:切线的判定,正方形的性质,旋转的性质
专题:证明题
分析:(1)①根据切线的性质由CH与⊙D相切得到∠CHD=90°,根据正方形的性质得∠ADC=90°,DA=DC,根据旋转的性质得∠GDH=90°,则利用同角的余角相等得∠ADG=∠CDH,再证明△ADG≌△CDH,得到∠AGD=∠CHD=90°,然后根据切线的判定定理得到AG与⊙D相切;
②作HE⊥CD于E,在Rt△CDH中,根据勾股定理出计算CH=2
,再根据面积法得
HE•CD=
CH•DH,即可计算出HE=
;
(2)当点H为CD⊙的交点时,点B到CH的距离最大,最大值为BC的长.
②作HE⊥CD于E,在Rt△CDH中,根据勾股定理出计算CH=2
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
(2)当点H为CD⊙的交点时,点B到CH的距离最大,最大值为BC的长.
解答:(1)①证明:∵CH与⊙D相切,
∴DH⊥CH,
∴∠CHD=90°,
∵四边形ABCD为正方形,
∴∠ADC=90°,DA=DC,
∵GD绕点D按顺时针方向旋转90°,
∴∠GDH=90°,
∴∠ADG+∠GDC=∠GDC+∠CDH,
∴∠ADG=∠CDH,
在△ADG和△CDH中
,
∴△ADG≌△CDH(SAS),
∴∠AGD=∠CHD=90°,
∴AG⊥DG,
∴AG与⊙D相切;
②解:作HE⊥CD于E,如图,
在Rt△CDH中,DH=2,CD=4,
∴CH=
=2
,
∵
HE•CD=
CH•DH,
∴HE=
=
;
(2)解:点B到CH的距离的最大值为4.
∴DH⊥CH,
∴∠CHD=90°,
∵四边形ABCD为正方形,
∴∠ADC=90°,DA=DC,
∵GD绕点D按顺时针方向旋转90°,
∴∠GDH=90°,
∴∠ADG+∠GDC=∠GDC+∠CDH,
∴∠ADG=∠CDH,
在△ADG和△CDH中

|
∴△ADG≌△CDH(SAS),
∴∠AGD=∠CHD=90°,
∴AG⊥DG,
∴AG与⊙D相切;
②解:作HE⊥CD于E,如图,
在Rt△CDH中,DH=2,CD=4,
∴CH=
| CD2-DH2 |
| 3 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴HE=
2×2
| ||
| 4 |
| 3 |
(2)解:点B到CH的距离的最大值为4.
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了切线的性质、旋转的性质和正方形的性质.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
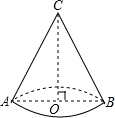 亮亮同学为了参加兰州市第十届中小学生艺术节,用纸板制作了一个圆锥形纸帽,如图所示,它的底面半径0B=9,高0C=12. 若不计损耗,则这个圆锥形纸帽的侧面积是
亮亮同学为了参加兰州市第十届中小学生艺术节,用纸板制作了一个圆锥形纸帽,如图所示,它的底面半径0B=9,高0C=12. 若不计损耗,则这个圆锥形纸帽的侧面积是( )
| A、90π | B、120π |
| C、135π | D、150π |
 如图:M为Rt△ABC斜边BC的中点,P、Q分别在边AB、BC上,且BP=5,CQ=3,PM⊥QM,则PQ=
如图:M为Rt△ABC斜边BC的中点,P、Q分别在边AB、BC上,且BP=5,CQ=3,PM⊥QM,则PQ= 根据马场的坐标为(-3,-3),建立直角坐标系,找到原点和x轴、y轴.再找到其他各景点的坐标.
根据马场的坐标为(-3,-3),建立直角坐标系,找到原点和x轴、y轴.再找到其他各景点的坐标.