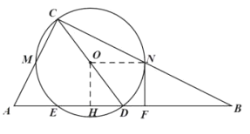
题目内容
【题目】如图,在![]() 中,
中,![]() ,以斜边
,以斜边![]() 上的中线
上的中线![]() 为直径作
为直径作![]() ,与
,与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,与
,与![]() 的另一个交点为
的另一个交点为![]() .过点
.过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
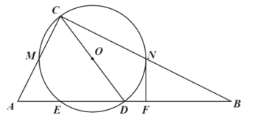
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求弦
,求弦![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接![]() ,ND,可知∠CND=90°,再证
,ND,可知∠CND=90°,再证![]() ,即可证
,即可证![]() ,最后根据切线的定义求得答案;
,最后根据切线的定义求得答案;
(2)根据勾股定理和![]() ,
,![]() ,可知
,可知![]() ,设
,设![]() 半径为
半径为![]() ,根据勾股定理可求出r值,过
,根据勾股定理可求出r值,过![]() 作
作![]() 于
于![]() ,则
,则![]() ,可知四边形
,可知四边形![]() 是矩形,从而可知OH,再次根据勾股定理即可求出DH,最后即可求出答案.
是矩形,从而可知OH,再次根据勾股定理即可求出DH,最后即可求出答案.
证明:(1)
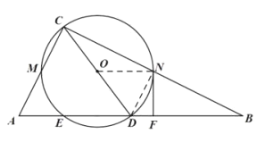
连接![]() ,
,![]() ,
,
在![]() 中,
中,![]() 为斜边中线,
为斜边中线,
∴![]() ,
,
∵![]() 是
是![]() 的直径.
的直径.
∴![]() ,
,
∴![]() ,
,
∵等腰![]() 三线合一,
三线合一,
∴![]() ,
,
∵在![]() 中,
中,![]() 为斜边
为斜边![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的半径,
的半径,
∴![]() 是
是![]() 的切线.
的切线.
(2)∵在![]() 中,
中,![]() 且
且![]() ,
,![]() ,
,
∴![]() ,
,
设![]() 半径为
半径为![]() ,
,
则![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
∵在等腰![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
过![]() 作
作![]() 于
于![]() ,
,
则![]() ,
,
由(1)可知∠ONF=∠NFH=90°
∴四边形![]() 是矩形,
是矩形,
则![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】某商场经营某种品牌的计算器,购进时的单价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是600个,而销售单价每上涨1元,就会少售出10个.
(1)不妨设该种品牌计算器的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y个和销售该品牌计算器获得利润w元,并把结果填写在表格中:
销售单价(元) | x(x>30) |
销售量y(个) |
|
销售计算器获得利润w(元) |
|
(2)在第(1)问的条件下,若计算器厂规定该品牌计算器销售单价不低于35元,且商场要完成不少于500个的销售任务,求:商场销售该品牌计算器获得最大利润是多少?