题目内容
6.(1)已知方程x2-3x-1=0的两根为x1和x2,求(x1-3)(x2-3)的值.(2)若关于x的一元二次方程x2-x+a-4=0的一根大于零、另一根小于零,求实数a的取值范围.
分析 (1)由条件利用韦达定理求得x1+x2 和x1x2的值,再根据(x1-3)( x2-3)=x1 x2 -3(x1+x2)+9,计算求得结果.
(2)一元二次方程x2-x+a-4=0的一根大于零,另一根小于零,则根的判别式大于0,两根之积小于0,解不等式即可.
解答 解:(1)∵方程x2-3x-1=0的两根为x1和x2,
∴x1+x2 =3,x1x2=-1,
故(x1-3)( x2-3)=x1 x2 -3(x1+x2)+9=-1-3×3+9=-1.
(2)根据题意,得:$\left\{\begin{array}{l}{1-4(a-4)>0}\\{a-4<0}\end{array}\right.$,
解得:a<4.
所以若关于x的一元二次方程x2-x+a-4=0的一根大于零,另一根小于零时,实数a的取值范围为:a<4.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的解和根与系数的关系.

练习册系列答案
相关题目
16. 如图,已知AB=AC,AD平分∠BAC,那么就可以证明△ABD≌△ACD,理由是( )
如图,已知AB=AC,AD平分∠BAC,那么就可以证明△ABD≌△ACD,理由是( )
 如图,已知AB=AC,AD平分∠BAC,那么就可以证明△ABD≌△ACD,理由是( )
如图,已知AB=AC,AD平分∠BAC,那么就可以证明△ABD≌△ACD,理由是( )| A. | SSS | B. | ASA | C. | SAS | D. | AAS |
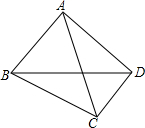 如图,四边形ABCD中,∠BAC=∠BCD=90°,若AC平分∠BCD,求证:AB=AD.
如图,四边形ABCD中,∠BAC=∠BCD=90°,若AC平分∠BCD,求证:AB=AD.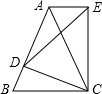 如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为底边,向上作等腰△DCE,使△EDC∽△ABC,连接AE.
如图,在等腰三角形ABC中,AB=AC,D是AB边上一点,以CD为底边,向上作等腰△DCE,使△EDC∽△ABC,连接AE.