题目内容
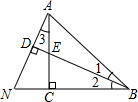 已知,如图,∠1=∠2,AD⊥BD于D,∠ACB=90°,AC=BC,证明:AD=
已知,如图,∠1=∠2,AD⊥BD于D,∠ACB=90°,AC=BC,证明:AD=| 1 |
| 2 |
考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:∠1=∠2,AD⊥BD,BD为公共边,可证明△ABD≌△NBD,所以AD=
AN,再由∠ACB=90°可得∠3=∠2,结合AC=BC,可证得△ACN≌△BCE,所以AN=BE,所以结论得证.
| 1 |
| 2 |
解答:证明:在Rt△ABD和Rt△NBD中,
,
∴△ABD≌△NBD(ASA),
∴AD=ND=
AN,
∵∠ACB=90°
∴∠3+∠AED=∠AED+∠2,
∴∠3=∠2,
在△ACN和△BCE中,
,
∴△ACN≌△BCE(ASA),
∴BE=AN,
∴AD=
BE.
|
∴△ABD≌△NBD(ASA),
∴AD=ND=
| 1 |
| 2 |
∵∠ACB=90°
∴∠3+∠AED=∠AED+∠2,
∴∠3=∠2,
在△ACN和△BCE中,
|
∴△ACN≌△BCE(ASA),
∴BE=AN,
∴AD=
| 1 |
| 2 |
点评:本题主要考查三角形全等的判定和性质,解题的关键是找到BE和AN之间的关系.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,在△ABC中,O为其内部一点,比较∠BOC和∠A的大小.
如图,在△ABC中,O为其内部一点,比较∠BOC和∠A的大小.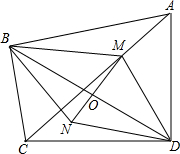 已知:如图所示,四边形ABCD中∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO并延长MO到N,使NO=MO,连接BN与ND.
已知:如图所示,四边形ABCD中∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO并延长MO到N,使NO=MO,连接BN与ND.
 已知,如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线交于点D.
已知,如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线交于点D.