题目内容
5.某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元.(1)求一根A型跳绳和一根B型跳绳的售价各是多少元?
(2)学校准备购进这两种型号的跳绳共50根,并且A型跳绳的数量不多于B型跳绳数量的3倍,请设计书最省钱的购买方案,并说明理由.
分析 (1)设一根A型跳绳售价是x元,一根B型跳绳的售价是y元,根据:“2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元”列方程组求解即可;
(2)首先根据“A型跳绳的数量不多于B型跳绳数量的3倍”确定自变量的取值范围,然后得到有关总费用和A型跳绳之间的关系得到函数解析式,确定函数的最值即可.
解答 解:(1)设一根A型跳绳售价是x元,一根B型跳绳的售价是y元,
根据题意,得:
$\left\{\begin{array}{l}{2x+y=56}\\{x+2y=82}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=10}\\{y=36}\end{array}\right.$,
答:一根A型跳绳售价是10元,一根B型跳绳的售价是36元;
(2)设购进A型跳绳m根,总费用为W元,
根据题意,得:W=10m+36(50-m)=-26m+1800,
∵-26<0,
∴W随m的增大而减小,
又∵m≤3(50-m),解得:m≤37.5,
而m为正整数,
∴当m=37时,W最小=-2×37+350=276,
此时50-37=13,
答:当购买A型跳绳37只,B型跳绳13只时,最省钱.
点评 此题主要考查了二元一次方程组的应用以及一次函数的应用等知识,根据题意得出正确的等量关系是解题关键.

练习册系列答案
相关题目
15.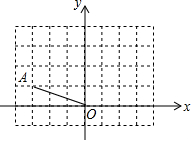 如图,在方格纸上建立的平面直角坐标系中,将OA绕原点O按顺时针方向旋转180°得到OA′,则点A′的坐标为( )
如图,在方格纸上建立的平面直角坐标系中,将OA绕原点O按顺时针方向旋转180°得到OA′,则点A′的坐标为( )
 如图,在方格纸上建立的平面直角坐标系中,将OA绕原点O按顺时针方向旋转180°得到OA′,则点A′的坐标为( )
如图,在方格纸上建立的平面直角坐标系中,将OA绕原点O按顺时针方向旋转180°得到OA′,则点A′的坐标为( )| A. | (-3,1) | B. | (1,-3) | C. | (1,3) | D. | (3,-1) |
16.若等腰三角形中相等的两边长为10cm,第三边长为12cm,那么第三边上的高为( )
| A. | 12 cm | B. | 10 cm | C. | 8 cm | D. | 6 cm |
10.下列说法中,正确的是( )
| A. | 真命题的逆命题是真命题 | |
| B. | 若原命题是假命题,则它的逆命题也是假命题 | |
| C. | 任何一个定理一定有逆定理 | |
| D. | 任何一个命题一定有逆命题 |
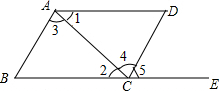 如图,下列能判断AB∥CD的条件有( )个
如图,下列能判断AB∥CD的条件有( )个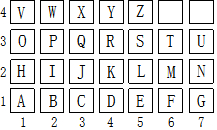 某个英文单词的字母顺序对应如上图中的有序数对分别为(6,2),(1,1),(6,3),(1,2),(5,3),请你把这个英文单词写出来为MATHS.
某个英文单词的字母顺序对应如上图中的有序数对分别为(6,2),(1,1),(6,3),(1,2),(5,3),请你把这个英文单词写出来为MATHS.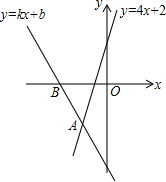 如图,直线y=kx+b经过点B(-2,0)与直线y=4x+2相交于点A,与y轴交于C(0,-4),则不等式4x+2<kx+b的解集为x<-1.
如图,直线y=kx+b经过点B(-2,0)与直线y=4x+2相交于点A,与y轴交于C(0,-4),则不等式4x+2<kx+b的解集为x<-1.