题目内容
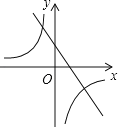
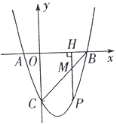
【题目】如图，一段抛物线：
，记为
，它与
轴交于点
，
；将绕点旋转
得
，交轴于点
；将绕点旋转得
，交轴于点
；…，如此进行下去，直至得
．
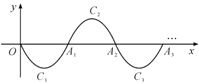
（1）请写出抛物线
的解析式：________；
（2）若
在第10段抛物线上，则
______．
【答案】
1
【解析】
（1）根据图象的旋转变化规律可得出旋转后函数的解析式，
（2）利用已知得出图象与
轴交坐标变化规律，进而求出
的值．
解：（1）
一段抛物线： 
，记为
，它与轴交于点
，
；
的图象过
，
两点，
∵将绕点旋转
得
，
抛物线的解析式二次项系数为：
，且过点，
，
同理得：抛物线
的解析式二次项系数为：1，且过点，
，抛物线
的解析式二次项系数为：，且过点，
，
抛物线的解析式为；
故答案为：；
（2）一段抛物线：，
图象与轴交点坐标为：，，
将绕点旋转得，交轴于点，，
将绕点
旋转得，交轴于，，
如此进行下去，直至得
．
的与轴的交点坐标为
，
，且图象在轴上方，
的解析式为：
，
把
代入得，
．
故答案为：1．
练习册系列答案
口算题天天练系列答案
相关题目
