题目内容
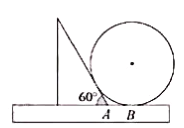
【题目】如图，一把直尺，
的直角三角板和光盘如图摆放，
为角与直尺交点，
,则光盘的直径是( )
A. 3 B. 
C. 
D. 
【答案】D
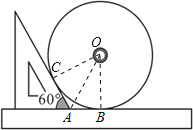
【解析】设光盘圆心为O，连接OC，OA，OB，由AC、AB都与圆O相切，利用切线长定理得到AO平分∠BAC，且OC垂直于AC，OB垂直于AB，可得出∠CAO=∠BAO=60°，得到∠AOB=30°，利用30°所对的直角边等于斜边的一半求出OA的长，再利用勾股定理求出OB的长，即可确定出光盘的直径．
如图，设光盘圆心为O，连接OC，OA，OB，
∵AC、AB都与圆O相切，
∴AO平分∠BAC，OC⊥AC，OB⊥AB，
∴∠CAO=∠BAO=60°，
∴∠AOB=30°，
在Rt△AOB中，AB=3cm，∠AOB=30°，
∴OA=6cm，
根据勾股定理得：OB=
3
，
则光盘的直径为6，
故选D.
练习册系列答案
相关题目
