题目内容
5. 如图,某校要用20m的篱笆,一面靠墙(墙长10m),围成一个矩形花圃,设矩形花圃垂直于墙的一边长为xm,花圃的面积为ym2.
如图,某校要用20m的篱笆,一面靠墙(墙长10m),围成一个矩形花圃,设矩形花圃垂直于墙的一边长为xm,花圃的面积为ym2.(1)求出y与x的函数关系式.
(2)当矩形花圃的面积为48m2时,求x的值.
(3)当边长x为多少时,矩形的面积最大,最大面积是多少?
分析 (1)根据面积=长•宽,求出长与宽即可解决.
(2)y=48代入(1),解方程即可.
(3)利用配方法,根据二次函数的性质确定最大值.
解答 解:(1)由题意Y=x(20-2x)=-2x2+20x.
(2)当y=48时,-2x2+20x=48,解得x=4或6,
经过检验x=4不合题意,
所以x=6.
(3)∵y=-2x2+20x=-2(x-5)2+50,
∴x=5时,y最大值=50.
点评 本题考查二次函数最值问题,关键是构建二次函数,利用函数的性质解决实际问题,易错的地方是忘了检验是否符合实际,属于中考常考题型.

练习册系列答案
相关题目
16.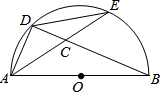 如图所示,AB是⊙O的直径,D、E是半圆上任意两点,连接AD、DE,AE与BD相交于点C,要是△ADC与△ABD相似,可以添加一个条件.下列添加的条件中错误的是( )
如图所示,AB是⊙O的直径,D、E是半圆上任意两点,连接AD、DE,AE与BD相交于点C,要是△ADC与△ABD相似,可以添加一个条件.下列添加的条件中错误的是( )
 如图所示,AB是⊙O的直径,D、E是半圆上任意两点,连接AD、DE,AE与BD相交于点C,要是△ADC与△ABD相似,可以添加一个条件.下列添加的条件中错误的是( )
如图所示,AB是⊙O的直径,D、E是半圆上任意两点,连接AD、DE,AE与BD相交于点C,要是△ADC与△ABD相似,可以添加一个条件.下列添加的条件中错误的是( )| A. | ∠ACD=∠DAB | B. | AD=DE | C. | AD•AB=CD•BD | D. | AD2=BD•CD |
13.不等式x-4<0的正整数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数多个 |
20.关于x的方程mx2-4x+4=0有解,则m的取值为( )
| A. | m≥1 | B. | m≤1 | C. | m≥1且m≠0 | D. | m≤1且m≠0 |
15.若a,b为实数,且|a+1|+$\sqrt{b-1}$=0,则(ab)2016的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | ±1 |
