题目内容
请完成下面的说明:(1)如图①所示,△ABC的外角平分线交于G,试说明∠BGC=90°- ∠A.
∠A.
说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____.
根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,
所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.
根据角平分线的意义,可知∠2+∠3= (∠EBC+∠FCB)=
(∠EBC+∠FCB)= (180°+∠_____)=90°+
(180°+∠_____)=90°+ ∠_______.
∠_______.
所以∠BGC=180°-(∠2+∠3)=90°-∠____.
(2)如图②所示,若△ABC的内角平分线交于点I,试说明∠BIC=90°+ ∠A.
∠A.
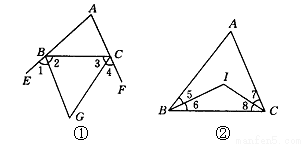
(3)用(1),(2)的结论,你能说出∠BGC和∠BIC的关系吗?
(1)A A A A A A;(2)证明见解析;(3)∠BGC和∠BIC互补.
【解析】
试题分析:(1)先根据三角形内角和定理可得出∠ABC+∠ACB=180°-∠A,再由平角的定义可得出∴∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠A)=180°+∠A,根据角平分线的定义即可得出结论;
(2)先根据三角形内角和等于180°可知∠ABC+∠ACB=180°-∠A,再由△ABC的内角平分线交于点I,
可知∠6+∠7= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (180°-∠A)=90°-
(180°-∠A)=90°- ∠A,故有∠BIG=180°-(∠6+∠8)即可得出结论.
∠A,故有∠BIG=180°-(∠6+∠8)即可得出结论.
(3)直接把两角相加即可得出结论.
试题解析:(1)∵根据三角形内角和等于180°,
∴∠ABC+∠ACB=180°-∠A.
∵平角是180°,
∴∠ABE+∠ACF=180°×2=360°,
∴∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠A)=180°+∠A.
∵△ABC的外角平分线交于G,
∴∠2+∠3= (∠EBC+∠FCB)=
(∠EBC+∠FCB)= (180°+∠A)=90°+
(180°+∠A)=90°+ ∠A,
∠A,
∴∠BGC=90°- ∠A.
∠A.
(2)证明:∵三角形内角和等于180°,
∴∠ABC+∠ACB=180°-∠A,
∵△ABC的内角平分线交于点I,
∴∠6+∠7= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (180°-∠A)=90°-
(180°-∠A)=90°- ∠A,
∠A,
∴∠BIC=180°-(∠6+∠8)
=180°-(90°- ∠A)
∠A)
=90°+ ∠A,
∠A,
即∠BIC=90°+ ∠A;
∠A;
(3)【解析】
∵由(1)、(2)知∠BGC=90°- ∠A,BIC=90°+
∠A,BIC=90°+ ∠A,
∠A,
∴∠BGC+∠BIC=90°- ∠A+90°+
∠A+90°+ ∠A=180°,
∠A=180°,
∴∠BGC和∠BIC互补.
考点:1.三角形内角和定理;2.三角形的角平分线、中线和高.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
 的对称轴是直线x=1
的对称轴是直线x=1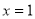 ,且图像经过点
,且图像经过点 (3,0),则
(3,0),则 的值为( )
的值为( )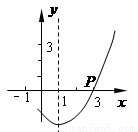
 ③;(2)①③
③;(2)①③ ②;(3)②③
②;(3)②③