题目内容
 如图,DE∥BC,且AD:DB=2:1,则△ADE与梯形DBCE的面积比为
如图,DE∥BC,且AD:DB=2:1,则△ADE与梯形DBCE的面积比为
- A.4:1
- B.4:9
- C.4:5
- D.1:4
C
分析:根据DE∥BC,即可求证△ADE∽△ABC,根据AD:DB即可求得△ADE与△ABC面积的计算,即可解题.
解答:∵DE∥BC,
∴△ADE∽△ABC,
∴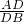 =
= ,
,
∵AD:DB=2:1,
∴AD:AB=2:3,
∴△ADE与△ABC的面积比为 =
= ,
,
∴△ADE与梯形DBCE的面积比为4:(9-4)=4:5.
故选C.
点评:本题考查了相似三角形的判定,相似三角形对应边比值相等的性质,本题中求证△ADE与△ABC的面积比是解题的关键.
分析:根据DE∥BC,即可求证△ADE∽△ABC,根据AD:DB即可求得△ADE与△ABC面积的计算,即可解题.
解答:∵DE∥BC,
∴△ADE∽△ABC,
∴
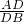 =
= ,
,∵AD:DB=2:1,
∴AD:AB=2:3,
∴△ADE与△ABC的面积比为
 =
= ,
,∴△ADE与梯形DBCE的面积比为4:(9-4)=4:5.
故选C.
点评:本题考查了相似三角形的判定,相似三角形对应边比值相等的性质,本题中求证△ADE与△ABC的面积比是解题的关键.

练习册系列答案
相关题目
 如图,DE∥BC,且DB=AE,若AB=5,AC=10,则AE的长为
如图,DE∥BC,且DB=AE,若AB=5,AC=10,则AE的长为 7、如图,DE∥BC,且AD:DB=2:1,则DE:BC=
7、如图,DE∥BC,且AD:DB=2:1,则DE:BC= 如图,DE∥BC,且AD=3,AB=5,CE=3,求AC的长.
如图,DE∥BC,且AD=3,AB=5,CE=3,求AC的长. 如图,DE∥BC,且
如图,DE∥BC,且 如图,DE∥BC,且AD:BD=3:1,则S△ADE:S梯形BCED=( )
如图,DE∥BC,且AD:BD=3:1,则S△ADE:S梯形BCED=( )