题目内容
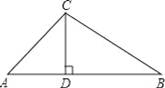
如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=1,则AB的长为 .

1+
 .
.
【考点】解直角三角形.
【专题】计算题.
【分析】在直角三角形BCD中,利用30度角所对的直角边等于斜边的一半,根据CD的长求出BC的长,利用勾股定理求出BD的长,在直角三角形ACD中,根据∠A的度数确定出此三角形为等腰直角三角形,得出AD=CD=1,由AD+DB即可求出AB的长.
【解答】解:在Rt△BCD中,∠B=30°,CD=1,
∴BC=2CD=2,
根据勾股定理得:BD=
 =
=
 ,
,
在Rt△ACD中,∠A=45°,CD=1,
∴AD=CD=1,
则AB=AD+DB=1+
 .
.
故答案为:1+
 .
.
【点评】此题考查了解直角三角形,涉及的知识有:勾股定理,锐角三角函数定义,含30度直角三角形的性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 则
则 ______;
______; _________.(结果精确到0.001)
_________.(结果精确到0.001) 有增根,那么a的值是______.
有增根,那么a的值是______.
 C.﹣3 D.﹣
C.﹣3 D.﹣


 (m3)的函数图像如图所示,那么ρ与
(m3)的函数图像如图所示,那么ρ与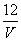 B. ρ=
B. ρ=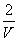 C. ρ=
C. ρ=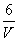 D.
D. 
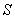 一定时,长
一定时,长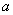 是宽
是宽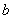 的反比例函数,其函数表达式可以写成
的反比例函数,其函数表达式可以写成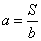 (
(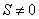 ).请你仿照上例另举出一个在日常生活、生产或学习中具有反比例函数关系的实例,并写出它的函数表达式.
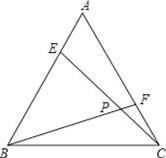
).请你仿照上例另举出一个在日常生活、生产或学习中具有反比例函数关系的实例,并写出它的函数表达式. °,则∠BFC的大小是( )°.(用含x的式子表示)
°,则∠BFC的大小是( )°.(用含x的式子表示) 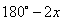 C. 180°-x D.2x
C. 180°-x D.2x