题目内容
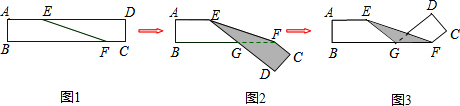
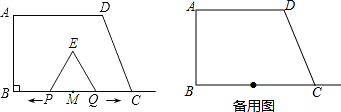
11.如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,AB=3$\sqrt{3}$,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).(1)设PQ的长为y,在点P从点M向点B运动的过程中,写出y与t之间的函数关系式(不必写t的取值范围).
(2)当BP=1时,求△EPQ与梯形ABCD重叠部分的面积.
(3)随着时间t的变化,线段AD会有一部分被△EPQ覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由.
分析 (1)由y=PM+QM列出函数关系式即可;
(2)当t=3或t=5时,BP=1,然后画出图形,计算即可;
(3)当t=4时,△EPQ的边长达到最大值,此后△EPQ沿射线BC平移,从而可求得t的取值范围.
解答 解:(1)y=PQ=PM+MQ=t+t=2t;
(2)如图1所示:连接EM.
当t=3时,PB=1.
∵PM=QM,
∴EM⊥PQ.
∵PB=1,
∴PM=QM=3.
∵△EPQ为等边三角形,
∴PE=6.
在Rt△EPQ中,ME=$\sqrt{P{E}^{2}-P{M}^{2}}=\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$.
∴点E在AD上.
∴△EPQ与梯形ABCD重叠部分的面积=${S}_{△EPQ}=\frac{1}{2}×6×3\sqrt{3}$=9$\sqrt{3}$.
如图2所示:过点E作EN⊥BQ,交AD于点G,EP交AD于点F.
当t=5时,PB=1时,
∵△EPQ为等边三角形,
∴PQ=PE=8,PN=QN=4.
在Rt△EPN中,EN=$\sqrt{P{E}^{2}-P{N}^{2}}=\sqrt{{8}^{2}-{4}^{2}}=4\sqrt{3}$,
∵DF∥PQ,
∴△EFD∽△EPQ.
∴$\frac{EG}{EN}=\frac{FD}{PQ}$.
∴$\frac{\sqrt{3}}{4\sqrt{3}}=\frac{DF}{8}$.
解得:DF=2.
∴△EPQ与梯形ABCD重叠部分的面积=$\frac{1}{2}(DF+PQ)AB=\frac{1}{2}×(2+8)×3\sqrt{3}$=15$\sqrt{3}$.
(3)能.
如图3所示;
当t=4时,△EPQ与△BCE′重合,此时线段AD被覆盖的长度到达最大值,
t=5时,△EPQ位于图中所示的位置,
∴4≤t≤5时,AD倍△EPQ覆盖部分的长度不变.
点评 本题主要考查的是四边形的综合应用、等腰三角形的性质、等边三角形的性质、勾股定理、三角形的面积公式、梯形的面积公式,根据题意画出图形是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 2-3 | B. | 2÷3 | C. | 23 | D. | 2-3 |
| x | 25 | 25.1 | 25.2 | 25.3 | 25.4 | 25.5 | 25.6 | 25.7 | 25.8 | 25.9 | 26 |
| x2 | 625 | 630.01 | 635.04 | 640.09 | 645.16 | 650.25 | 655.36 | 660.49 | 665.64 | 670.81 | 676 |
(2)$\sqrt{670.8}$=25.9.
(3)25.2<$\sqrt{640}$<25.3.
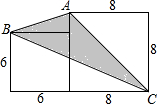 如图,求阴影部分的面积.
如图,求阴影部分的面积.