题目内容
化简求值：（2a+b+1）（2a-b-1）-（a+2b）（-2b+a）+2b，其中a、b满足|a+b-3|+（ab+2）2=0．
考点：整式的混合运算—化简求值,非负数的性质：绝对值,非负数的性质：偶次方
专题：计算题
分析：原式第一项利用平方差公式化简，再利用完全平方公式展开，第二项利用平方差公式化简，去括号合并得到最简结果，利用非负数的性质求出a+b与ab得分值，利用完全平方公式求出a2+b2的值，代入计算即可求出值．
解答：解：原式=4a2-b2-2b-1-a2+4b2+2b=3（a2+b2）-1，
∵|a+b-3|+（ab+2）2=0，
∴a+b=3，ab=-2，
将a+b=3两边平方得：（a+b）2=a2+b2+2ab=9，
把ab=-2代入得：a2+b2=13，
则原式=39-1=38．
∵|a+b-3|+（ab+2）2=0，
∴a+b=3，ab=-2，
将a+b=3两边平方得：（a+b）2=a2+b2+2ab=9，
把ab=-2代入得：a2+b2=13，
则原式=39-1=38．
点评：此题考查了整式的混合运算-化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
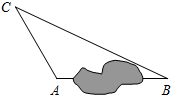在一次课外实践活动中，同学们要知道校园内A、B两处的距离，但无法直接测得．已知校园内A、B、C三点形成的三角形如图所示，并测得AC=60m，BC=140m，∠CAB=120°，请计算A、B两处之间的距离．