题目内容
 如图,AB为圆的直径.若AB=AC=5,BD=4,则
如图,AB为圆的直径.若AB=AC=5,BD=4,则 的值为
的值为
- A.

- B.

- C.
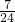
- D.
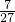
C
分析:连AD,得到∠E=90°,AD⊥BC,则AD平分BC,由此可求出AD=3,DC=4,BC=8,易证直角△CDA~直角△CEB,利用相似比即可求出BE,CA,这样就可得到AE,最后计算 的值.
的值.
解答: 解:连AD,如图,
解:连AD,如图,
∵AB为圆的直径,
∴∠E=90°,AD⊥BC,
而AB=AC=5,BD=4,则AD=3,BD=DC,
∴AD平分BC,即BC=2BD=8,
∵∠C公共,
∴直角△CDA∽直角△CEB,
∴ =
= =
=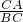 ,即
,即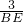 =
= =
= ,
,
所以BE= ,CE=
,CE= ,则AE=
,则AE= -5=
-5= ,
,
所以 =
=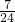 .
.
故选C.
点评:本题考查了圆周角定理:在同圆和等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查直径所对的圆周角为90度、等腰三角形的性质以及相似三角形的判定与性质.
分析:连AD,得到∠E=90°,AD⊥BC,则AD平分BC,由此可求出AD=3,DC=4,BC=8,易证直角△CDA~直角△CEB,利用相似比即可求出BE,CA,这样就可得到AE,最后计算
 的值.
的值.解答:
 解:连AD,如图,
解:连AD,如图,∵AB为圆的直径,
∴∠E=90°,AD⊥BC,
而AB=AC=5,BD=4,则AD=3,BD=DC,
∴AD平分BC,即BC=2BD=8,
∵∠C公共,
∴直角△CDA∽直角△CEB,
∴
 =
= =
=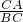 ,即
,即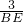 =
= =
= ,
,所以BE=
 ,CE=
,CE= ,则AE=
,则AE= -5=
-5= ,
,所以
 =
=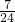 .
.故选C.
点评:本题考查了圆周角定理:在同圆和等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查直径所对的圆周角为90度、等腰三角形的性质以及相似三角形的判定与性质.

练习册系列答案
相关题目
 如图,AB为圆的直径.若AB=AC=5,BD=4,则
如图,AB为圆的直径.若AB=AC=5,BD=4,则| AE |
| BE |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,AB为圆的直径.若AB=AC=5,BD=4,则tan∠ABE=
如图,AB为圆的直径.若AB=AC=5,BD=4,则tan∠ABE=

