题目内容
9.已知y=(k+2)${x}^{{k}^{2}+k-4}$+2x+3是二次函数,且函数图象有最高点.(1)求k的值和顶点坐标.
(2)若图象与x轴交点为A.B,与y轴交点为C,求△ABC面积.
(3)若以AB为直径的圆D与y轴相交于点E,求点E的坐标.
分析 (1)根据二次函数的定义得出k2+k-4=2,再利用函数图象有最高点,得出k+2<0,即可得出k的值,利用k的值得出二次函数的解析式,利用顶点式求出二次函数顶点坐标;
(2)求出(1)中抛物线与x轴、y轴的交点坐标,即可计算△ABC面积;
(3)根据A、B的坐标,可知圆心D的坐标,根据勾股定理求出OE的长,可确定点E的坐标.
解答 解:(1)∵y=(k+2)xk2+k-4+2x+3是二次函数,
∴k2+k-4=2,
k2+k-6=0,
∴(k+3)(k-2)=0,
∴k=-3或k=2,
∵函数图象有最高点,
∴k+2<0,
当k=-3时,k+2=-1<0,符合要求,
当k=2时,k+2=4>0,不符合要求,舍去;
∴二次函数解析式为:y=-x2+2x+3=-(x-1)2+4,
∴顶点坐标为:(1,4);
(2)令y=0,则0=-x2+2x+3,解得x1=-1,x2=3,
∴AB=4,
当x=0时,y=3,
∴OC=3
∴S△ABC=$\frac{1}{2}$×4×3=6;
(3)∵A(-1,0),B(3,0)
∴D(1,0)
∵以AB为直径的圆D与y轴相交于点E,
∴OD=1,DE=2,
∴OE=$\sqrt{3}$,
∴点E的坐标为(0,$\sqrt{3}$)或(0,-$\sqrt{3}$).
点评 本题主要考查了二次函数的定义、二次函数上点的坐标以及数形结合思想和分类讨论思想的运用,求出抛物线与坐标轴的交点坐标是解决问题的关键.

练习册系列答案
相关题目
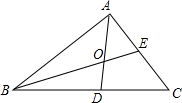 如图,在△ABC中,DC:BC=1:3,BO:OE=4:1,那么CE:EA=1.
如图,在△ABC中,DC:BC=1:3,BO:OE=4:1,那么CE:EA=1. 如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC为斜边AC为直角边,画第2个等腰直角三角形ACD,再以Rt△ACD的斜边AD为直角边,画第3个等腰直角三角形ADE…,以此类推,则第15个等腰直角三角形的斜边长为128$\sqrt{2}$.
如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC为斜边AC为直角边,画第2个等腰直角三角形ACD,再以Rt△ACD的斜边AD为直角边,画第3个等腰直角三角形ADE…,以此类推,则第15个等腰直角三角形的斜边长为128$\sqrt{2}$.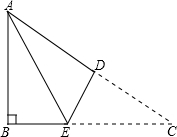 如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长=7cm.
如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长=7cm.