题目内容
如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.
(1)判断直线PF与AC的位置关系,并说明你的理由;
(2)当⊙O的半径为5,tan∠P=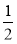 ,求AC的长.
,求AC的长.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
题目内容
如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.
(1)判断直线PF与AC的位置关系,并说明你的理由;
(2)当⊙O的半径为5,tan∠P=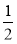 ,求AC的长.
,求AC的长.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案