题目内容
3.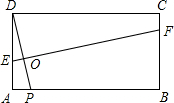 如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.当x=0,折痕EF的长为3,当点E与点A重合时,折痕EF的长为$\sqrt{2}$.
如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.当x=0,折痕EF的长为3,当点E与点A重合时,折痕EF的长为$\sqrt{2}$.
分析 当x=0时,折痕EF的长正好等于矩形的长为3,当点E与点A重合时,画出符合要求的图形,得出∠DEF=∠FEP=45°,利用勾股定理得出答案.
解答 解:∵纸片折叠,使点D与点P重合,得折痕EF,
当AP=x=0时,点D与点P重合,
即为A,D重合,B,C重合,
那么EF=AB=CD=3;
当点E与点A重合时,如图所示: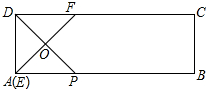
∵点D与点P重合是已知条件,
∴∠DEF=∠FEP=45°,
∴∠DFE=45°,
即:ED=DF=1,
利用勾股定理得出EF=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$
∴折痕EF的长为$\sqrt{2}$;
故答案为:3,$\sqrt{2}$;
点评 此题主要考查了矩形的性质、折叠的性质、勾股定理的应用;根据已知条件得出对应线段与对应角之间的关系是解决问题的关键.

练习册系列答案
相关题目
13.相反数与绝对值相等的数是( )
| A. | 正数 | B. | 负数 | C. | 非负数 | D. | 非正数 |
12.以下列各组长度的线段为边,能构成三角形的是( )
| A. | 3,4,5 | B. | 7,3,4 | C. | 5,6,12 | D. | 1,2,3 |
 在平面直角坐标系中,O为坐标原点,抛物线y=-x2+kx+4与y轴交于A,与x轴的负半轴交于B,且△ABO的面积是8.
在平面直角坐标系中,O为坐标原点,抛物线y=-x2+kx+4与y轴交于A,与x轴的负半轴交于B,且△ABO的面积是8.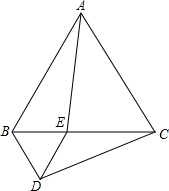 如图,等边三角形ABC的边长为4,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD.
如图,等边三角形ABC的边长为4,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD. 如图,已知△ABC≌△DBE,如果∠CBD=96°,∠CBE=28°,那么∠ABC=68°.
如图,已知△ABC≌△DBE,如果∠CBD=96°,∠CBE=28°,那么∠ABC=68°.