题目内容
7.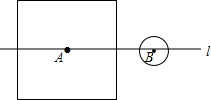 如图,直线l过边长为10的正方形中心A,且与正方形的一组对边平行,B在直线l上,AB=7,圆B的半径等于r.
如图,直线l过边长为10的正方形中心A,且与正方形的一组对边平行,B在直线l上,AB=7,圆B的半径等于r.(1)当r=2时,圆与正方形只有1个公共点;
(2)当圆与正方形有2个公共点时,求r的取值范围;
(3)圆与正方形公共点的个数还有其他情况吗?如果有,请写出相应的r的取值范围.
分析 (1)根据圆心到直线的距离等于半径时,直线与圆有一个公共点,求出r的范围;
(2)求出圆与正方形的右边和左边相切时的半径,在这个范围内⊙B和正方形的边都有2个公共点;当圆的半径为点B到左边顶点距离时,也有两个公共点;
(3)根据题意和图形可知,圆与正方形公共点的个数可能是0、3、4个,写出相应的r的取值范围即可.
解答 解:(1)圆与正方形的右边相切时,r=AB-5=2,
∴r=2时,圆与正方形只有1个公共点;
(2)圆与正方形左边相切时,r=AB+5=12,
∴2<r<12,
当公共点是右边顶点时,r=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
所以,r的取值范围是2<r<12或r=13.
(3)当0<r<2或r>13时,圆与正方形没有公共点;
当r=12时,圆与正方形有3个公共点;
当12<r<13时,圆与正方形有4个公共点.
点评 本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定.

练习册系列答案
相关题目
17.估计$\sqrt{5}$+1在( )
| A. | 0~1之间 | B. | 1~2之间 | C. | 2~3之间 | D. | 3~4之间 |
18.如果四个不同的整数m,n,p,q满足(5-m)(5-n)(5-p)(5-q)=4,则m+n+p+q等于( )
| A. | 4 | B. | 10 | C. | 12 | D. | 20 |
2.下列图形中,阴影部分面积为1的是( )
| A. |  | B. |  | C. |  | D. |  |
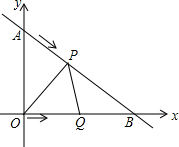 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与坐标轴交于A,B两点,设P,Q分别为AB边,OB边上的动点,它们同时分别从点A,点O以每秒1个单位速度向终点B匀速移动,当一个点到达终点时另一个点也停止移动,设移动时间为t秒.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与坐标轴交于A,B两点,设P,Q分别为AB边,OB边上的动点,它们同时分别从点A,点O以每秒1个单位速度向终点B匀速移动,当一个点到达终点时另一个点也停止移动,设移动时间为t秒.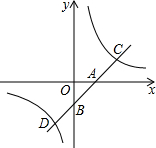 如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,-1),交双曲线y=$\frac{2}{x}$于点C、D.
如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,-1),交双曲线y=$\frac{2}{x}$于点C、D.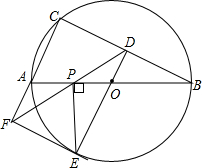 如图,⊙O是△ABC的外接圆,AB是直径,过点O作OD⊥CB,垂足为点D,延长DO交⊙O于点E,过点E作PE⊥AB,垂足为点P,作射线DP交CA的延长线于F点,连接EF,
如图,⊙O是△ABC的外接圆,AB是直径,过点O作OD⊥CB,垂足为点D,延长DO交⊙O于点E,过点E作PE⊥AB,垂足为点P,作射线DP交CA的延长线于F点,连接EF,