题目内容
12.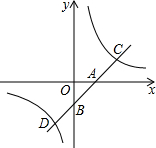 如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,-1),交双曲线y=$\frac{2}{x}$于点C、D.
如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,-1),交双曲线y=$\frac{2}{x}$于点C、D.(1)求k、b的值;
(2)写出不等式kx+b>$\frac{2}{x}$的解集.
分析 (1)把A、B的坐标代入一次函数的解析式,即可求出k、b;
(2)解由两函数组成的方程组,求出方程组的解即可得出C、D的坐标;根据图象和D、C的坐标即可得出答案.
解答 解:(1)∵直线y=kx+b过点(1,0)和(0,-1),
∴$\left\{\begin{array}{l}{0=k+b}\\{-1=b}\end{array}\right.$,
∴k=1,b=-1,
(2)解$\left\{\begin{array}{l}{y=x-1}\\{y=\frac{2}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
∴C(2,1),D(-1,-2),
∴不等式kx+b>$\frac{2}{x}$的解集是:x>2或-1<x<0.
点评 本题考查了一次函数和反比例函数的交点问题,用待定系数法求函数的解析式,函数的图象,主要考查学生的理解能力和计算能力,题目比较好,难度适中.

练习册系列答案
相关题目
2. 如图,已知直线a,b被直线c所截,那么∠1的内错角是( )
如图,已知直线a,b被直线c所截,那么∠1的内错角是( )
 如图,已知直线a,b被直线c所截,那么∠1的内错角是( )
如图,已知直线a,b被直线c所截,那么∠1的内错角是( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
3.把多项式2x2-18分解因式,结果正确的是( )
| A. | 2(x2-9) | B. | 2(x+9)(x-9) | C. | 2(x+3)(x-3) | D. | 2(x-3)2 |
17.已知命题“关于x的一元二次方程x2+bx+1=0,当b<0时必有实数解”,能说明这个命题是假命题的一个反例是( )
| A. | b=0 | B. | b=-1 | C. | b=2 | D. | b=-2 |
2.一个直角三角形两条直角边的长分别为4,8,另一个和它相似的直角三角形的一条直角边为12,则另一条直角边的长为( )
| A. | 6 | B. | 24 | C. | 6或24 | D. | 6$\sqrt{5}$或$\sqrt{10}$ |
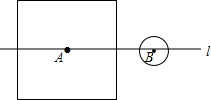 如图,直线l过边长为10的正方形中心A,且与正方形的一组对边平行,B在直线l上,AB=7,圆B的半径等于r.
如图,直线l过边长为10的正方形中心A,且与正方形的一组对边平行,B在直线l上,AB=7,圆B的半径等于r.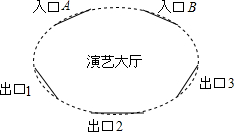 某演艺大厅有2个入口和3个出口,其示意图如下,参观者从任意一个入口进入,参观结束后从任意一个出口离开
某演艺大厅有2个入口和3个出口,其示意图如下,参观者从任意一个入口进入,参观结束后从任意一个出口离开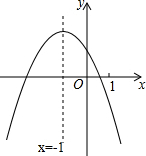 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论: