题目内容
18.如果四个不同的整数m,n,p,q满足(5-m)(5-n)(5-p)(5-q)=4,则m+n+p+q等于( )| A. | 4 | B. | 10 | C. | 12 | D. | 20 |
分析 因为m,n,p,q都是四个不同正整数,所以(5-m)、(5-n)、(5-p)、(5-q)都是不同的整数,四个不同的整数的积等于4,这四个整数为(-1)、(-2)、1、2,由此求得m,n,p,q的值,问题得解.
解答 解:因为(5-m)(5-n)(5-p)(5-q)=4,
每一个因数都是整数且都不相同,
那么只可能是-1,1,-2,2,
由此得出m、n、p、q分别为6、4、7、3,所以,m+n+p+q=20.
故选:D.
点评 本题考查了有理数的乘法,解决本题的关键是一个正整数通过分解把它写为四个不同的整数的乘积,要考虑有两个正因数,两个负因数,从而再结合题意解决问题.

练习册系列答案
相关题目
9.下列选项不正确的是( )
| A. | 两直线平行,同位角相等 | |
| B. | 对顶角相等 | |
| C. | ∵∠1=∠2,∠2=∠3,∴∠1=∠3 | |
| D. | 两条直线被第三条直线所截,同旁内角互补 |
6.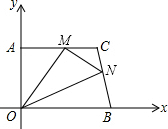 在平面直角坐标系中,直角梯形AOBC的位置如图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别在线段AC、线段BC上运动,当△MON的面积达到最大时,存在一种使得△MON周长最小的情况,则此时点M的坐标为( )
在平面直角坐标系中,直角梯形AOBC的位置如图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别在线段AC、线段BC上运动,当△MON的面积达到最大时,存在一种使得△MON周长最小的情况,则此时点M的坐标为( )
 在平面直角坐标系中,直角梯形AOBC的位置如图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别在线段AC、线段BC上运动,当△MON的面积达到最大时,存在一种使得△MON周长最小的情况,则此时点M的坐标为( )
在平面直角坐标系中,直角梯形AOBC的位置如图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别在线段AC、线段BC上运动,当△MON的面积达到最大时,存在一种使得△MON周长最小的情况,则此时点M的坐标为( )| A. | (0,4) | B. | (3,4) | C. | ($\frac{5}{2}$,4) | D. | ($\sqrt{3}$,3) |
13.下列各式中正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\root{3}{64}$=4 | C. | $\sqrt{-9}$=3 | D. | $\sqrt{2\frac{1}{4}}$=$\frac{3}{4}$ |
3.把多项式2x2-18分解因式,结果正确的是( )
| A. | 2(x2-9) | B. | 2(x+9)(x-9) | C. | 2(x+3)(x-3) | D. | 2(x-3)2 |
8.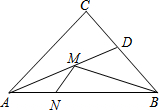 如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
 如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )| A. | $3\sqrt{2}$ | B. | 4 | C. | $4\sqrt{2}$ | D. | 6 |
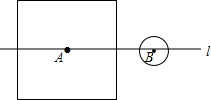 如图,直线l过边长为10的正方形中心A,且与正方形的一组对边平行,B在直线l上,AB=7,圆B的半径等于r.
如图,直线l过边长为10的正方形中心A,且与正方形的一组对边平行,B在直线l上,AB=7,圆B的半径等于r.