题目内容
3．
a、b在数轴上所表示的点如图所示，化简：$\sqrt{{a}^{2}b}$=-a$\sqrt{b}$．
分析 根据数轴确定a和b的符号，然后根据二次根式的性质化简．
解答 解：根据数轴可得a＜0，b＞0，
则原式=|a|$\sqrt{b}$=-a$\sqrt{b}$．
故答案是：-a$\sqrt{b}$．
点评 本题考查了二次根式的化简，正确理解$\sqrt{{a}^{2}}$=|a|=$\left\{\begin{array}{l}{a（a≥0）}\\{-a（a＜0）}\end{array}\right.$是关键．
练习册系列答案
相关题目
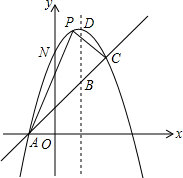如图，已知抛物线y=-x2+bx+c过（1，4）与（4，-5）两点，且与一直线y=x+1相交于A，C两点，
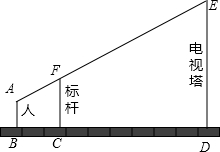如图，某测量工作人员与标杆顶端F、电视塔顶端在同一直线上，已知此人眼睛距地面1.6米，标杆为3.2米，且BC=1米，CD=5米，则电视塔的高ED=11.2．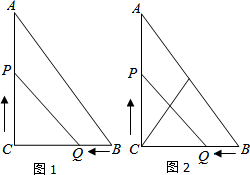
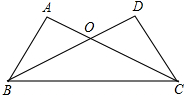如图，∠A=∠D，OA=OD，∠DOC=50°，则∠DBC=25度．