题目内容
7.如图,点A、B在直线MN上,AB=11cm,⊙A、⊙B的半径为1cm.⊙A以每秒2cm的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0).(1)当t=1时,AB=9cm;当t=6时,AB=1cm;
(2)问点A出发后多少秒两圆相切?

分析 (1)当t=1时,点A在点B的左侧,易得AB=9cm;当t=6时,点A在点B的右侧,易得AB=1cm;
(2)点A在点B的左侧时,圆心距为11-2t;点A在点B的右侧时,圆心距为2t-11,然后根据外切、内切的判定方法得到1+1+t=11-2t;1+t-1=11-2t;1+t-1=2t-11;1+1+t=2t-11;再分别解关于t的方程即可.
解答 解:(1)当t=1时,AB=11-2t=11-2=9(cm);
当t=6时,AB=2t-11=2×6-11(cm);
故答案为9,1;
(2)当⊙A与⊙B在点B的左侧外切时,1+1+t=11-2t,解得t=3(s);
当⊙A与⊙B在点B的左侧内切时,1+t-1=11-2t,解得t=$\frac{11}{3}$(s);
当⊙A与⊙B在点B的右侧内切时,1+t-1=2t-11,解得t=11(s);
当⊙A与⊙B在点B的右侧外切时,1+1+t=2t-11,解得t=13(s),
综上所述,点A出发后3s或$\frac{11}{3}$s或11s或13s时两圆相切.
点评 本题考查了圆与圆的位置关系:两圆的圆心距为d,两圆半径分别为R,r,则:两圆外离?d>R+r;两圆外切?d=R+r;两圆相交?R-r<d<R+r(R≥r);两圆内切?d=R-r(R>r);两圆内含?d<R-r(R>r).注意分类讨论思想的运用.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
16.下列各组不是同类项的是( )
| A. | a2b3与-5a2b3 | B. | $\frac{1}{2}$xy2与4y2x | C. | 2x2y与2xy2 | D. | -3与π |
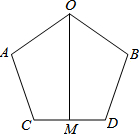 已知:OA=OB,AC=BD,∠A=∠B,M为CD中点.求证:OM平分∠AOB.
已知:OA=OB,AC=BD,∠A=∠B,M为CD中点.求证:OM平分∠AOB.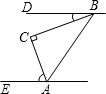 如图,在△ABC中,∠C=90°.若BD∥AE,则∠DBC+∠CAE的度数是90°.
如图,在△ABC中,∠C=90°.若BD∥AE,则∠DBC+∠CAE的度数是90°.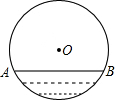 如图,水平放置的一个油管的截面半径为13cm,其中有油部分油面宽AB为24cm,求油的最大深度.
如图,水平放置的一个油管的截面半径为13cm,其中有油部分油面宽AB为24cm,求油的最大深度.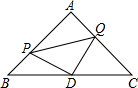 如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.
如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.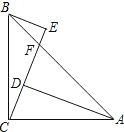 如图,已知∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,CE与AB相交于F.
如图,已知∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,CE与AB相交于F.