题目内容
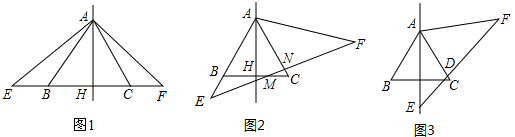
11.已知△ABC是等边三角形,△AEF是等腰三角形,点B,C在EF上,且∠E=40°.(1)如果△ABC和△AEF有公共的对称轴AH,求∠EAB的度数;
(2)如果绕A点固定转动△AEF,使AE与AB在一条直线上,那么EF与BC交于M点,EF与AE交于N点,求∠EMB的度数,并说明△ANF的形状;
(3)如果继续转动△AEF,使AE与AH在一条直线上,EF与AC交于D,请判断△ADF的形状,并说明理由.
分析 (1)根据等边三角形的性质和外角的性质即可得到结果;
(2)根据外角的性质和等边三角形的性质,得到△ANF的各个内角的度数,从而判断出其形状;
(3)根据轴对称的性质求出∠CAH的度数,利用外角的性质和三角形的内角和求出△AFD的内角的度数,于是结论可得.
解答 解:(1)∵△ABC是等边三角形,
∴∠ABC=60°,
∵∠E=40°,
∴∠EAB=20°;
(2)∵AE与AB在一条直线上,
∴∠ABC=∠E+∠BME=60°,
∴∠EMB=∠ABC-∠E=20°,
∵△AEF是等腰三角形,
∴∠F=∠E=40°,
∠ANF=∠BAC+∠E=80°,
∴∠NAF=60°,
∴△ANF是锐角三角形;
(3)∵AE与AH在一条直线上,
∴∠EAC=30°,
∴∠ADE=∠EAD+∠E=70°,
∵∠F=∠E=40°,
∴∠FAD=70°,
∴∠FAD=∠FDA,
∴△AFD是等腰三角形.
点评 本题考查了等腰三角形的性质和判定,等边三角形的性质,轴对称的性质,熟练掌握各定理是解题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
3.某工厂生产一批螺帽,根据产品质量要求,螺帽的内径可以有0.02毫米误差,抽查5只螺帽,超过规定内径的毫米数记为正数,不足规定内径的毫米数记为负数,检查结果如下表.
(1)指出哪些产品是合乎要求的(即在误差范围内的)
(2)指出合乎要求的产品中哪个质量好一些,并用绝对值的知识进行说明.
| +0.030 | -0.018 | +0.026 | -0.025 | +0.015 |
(2)指出合乎要求的产品中哪个质量好一些,并用绝对值的知识进行说明.
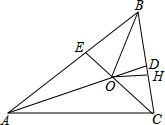 已知:如图,在△ABC中,∠BAC、∠BCA的角平分线AD、CE相交于点O.OH⊥BC于点H,连接OB.
已知:如图,在△ABC中,∠BAC、∠BCA的角平分线AD、CE相交于点O.OH⊥BC于点H,连接OB.