题目内容
9.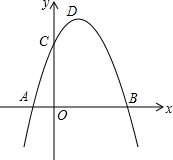 如图,已知抛物线 y=-x2+mx+4m 的图象与x轴交于A、B两点,与y轴交于点C(0,8).
如图,已知抛物线 y=-x2+mx+4m 的图象与x轴交于A、B两点,与y轴交于点C(0,8).(1)求抛物线的解析式,并写出顶点D的坐标;
(2)抛物线上是否存在点E,使△ABE的面积为15?若存在,请求出所有符合条件E的坐标;若不存在,请说明理由;
(3)连结BD,动点P在线段BD上运动(不含端点B、D),连结CP,过点P作x轴的垂线,垂足为H,设OH的长度为t,四边形PCOH的面积为S.试探究:四边形PCOH的面积S有无最大值?如果有,请求出这个最大值;如果没有,请说明理由.
分析 (1)只需把点C的坐标代入抛物线的解析式,就可求出抛物线的解析式,然后用配方法就可求出顶点D的坐标;
(2)可先求出A、B两点的坐标,得到AB的值,根据△ABE的面积可求出点E的纵坐标,代入抛物线的解析式,就可求出点E的坐标;
(3)可先求出DB的解析式,从而得到PH(用t的代数式表示),然后用t的代数式表示出梯形PCOH的面积,再运用配方法就可解决问题.
解答 解:(1)∵点C(0,8)在抛物线y=-x2+mx+4m 上,
∴4m=8,
∴m=2,
∴抛物线的解析式为y=-x2+2x+8.
∵y=-x2+2x+8=-(x-1)2+9,
∴顶点D的坐标为(1,9);
(2)令y=0,则-x2+2x+8=0,
解得:x1=4,x2=-2,
∴A(-2,0),B(4,0),
∴OA=2,OB=4,AB=6.
∵S△ABE=$\frac{1}{2}$×AB×|yE|=3|yE|=15,
∴yE=±5.
当yE=5时,-x2+2x+8=5,
解得:x3=3,x4=-1.
当yE=-5时,-x2+2x+8=-5,
解得:x5=1+$\sqrt{14}$,x6=1-$\sqrt{14}$.
∴点E的坐标为(3,5),(-1,5),(1+$\sqrt{14}$,-5),(1-$\sqrt{14}$,-5);
(3)设DB的解析式为y=kx+b,
则有$\left\{\begin{array}{l}{k+b=9}\\{4k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-3}\\{b=12}\end{array}\right.$,
∴DB的解析式为y=-3x+12.
∵OH=t,
∴P(t,-3t+12),PH=-3t+12,
∴S=$\frac{1}{2}$(8-3t+12)t=-$\frac{3}{2}$t2+10t=-$\frac{3}{2}$(t-$\frac{10}{3}$)2+$\frac{50}{3}$.
∵1<t<4,
∴当t=$\frac{10}{3}$时,S最大=$\frac{50}{3}$.
点评 本题主要考查了用待定系数法求抛物线及直线的解析式、解一元二次方程等知识,运用配方法是解决本题的关键,需要注意的是点E到x轴的距离为|yE|,而不是yE.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案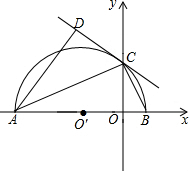 如图所示,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半⊙Oˊ与y轴正半轴交于点C,连接BC,AC.CD是半⊙Oˊ的切线,AD⊥CD于点D.
如图所示,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半⊙Oˊ与y轴正半轴交于点C,连接BC,AC.CD是半⊙Oˊ的切线,AD⊥CD于点D.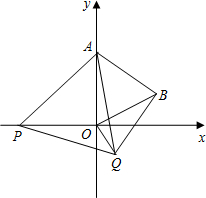 如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记点Q的位置为B,则当点P从(-2,0)运动到(2,0)时,点Q运动的路径长为4.
如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记点Q的位置为B,则当点P从(-2,0)运动到(2,0)时,点Q运动的路径长为4.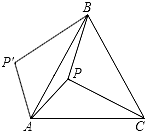 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB=150°,△ABC的面积=36+25$\sqrt{3}$.
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB=150°,△ABC的面积=36+25$\sqrt{3}$.